Mathématiques 2: Perimètre, aire et volume
Le périmètre est la mesure du contour: P
L'aire est la mesure de la surface: A
Le volume est la mesure de l'espace occupé: V
1. Carré
c est le côté du carré
P = 4 c
A = c x c = c2

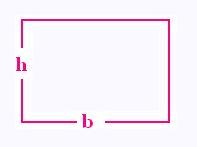
2. Rectangle
b base, h hauteur du rectangle
P = 2(b + h)
A = b h
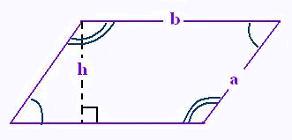
3. Parallélogramme
a largeur, b longeur et h hauteur du parallélogramme
P = 2(a + b)
A = b h
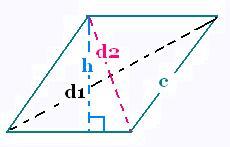
4. Lozange
d1, d1 diagonales, c côté,
et h hauteur du lozange
P = 4 c
A = d1 d2/2 = c h
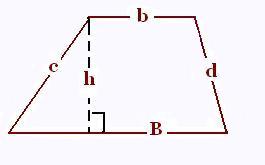
5. Trapèze
B grande base, b petite base, h hauteur, c et d côtés
opposés du trapèze
P = B + b + c + d
A = h (B + b)/2
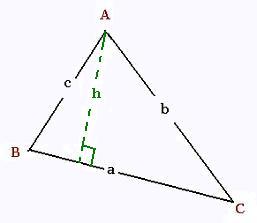
6. Triange quelconque
a, b et c côtés, h hauteur du triangle
P = a + b + c
A = ah/2
Hauteur extérieure
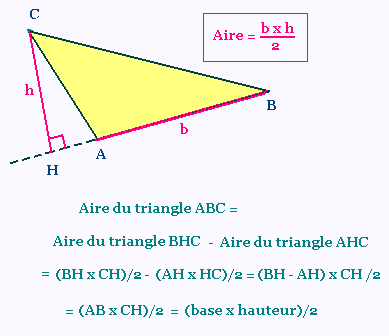
Même dans le cas où la hauteur est extérieure
au triangle ,
l'aire du triangle reste égale à
(base x hauteure)/2.
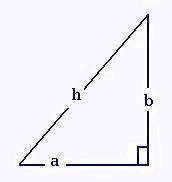
7. Triange rectangle
a, b côtés, et h hypoténuse
du triangle rectangle
P = a + b + h
A = ab/2
Théorème de Pythagore: a2 + b2 = h2
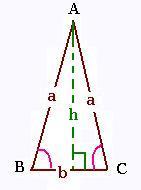
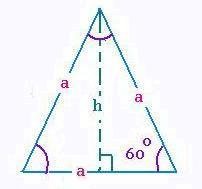
8. Triange isocèle
a côtés, b base et h hauteur
du triangle isocèle
P = 2a + b
A = bh/2
9. Triange équilatéral
a côtés et h hauteur
du triangle équilatéral
P = 3a
A = ah/2
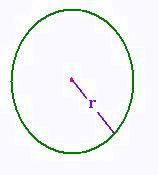
10. Cercle
r rayon du cercle
P = Circonférence = 2πr
A = πr2
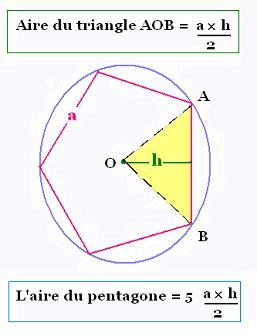
11. Polygone régulier
a côté, h l'apothème du polygone
Pentagone:
P = 5 a
A = 5 x (aire du triangle isocèle) = 5 ah/2
Généralisation: Polygone régulier de n côtés:
P = n a
A = n x (aire du triangle isocèle) = n ah/2
Pentagone: n = 5 , P = 5 a , A = 5 ah/2
Hexagone: n = 6 , P = 6 a , A = 6 ah/2
Heptagone: n = 5 , P = 5 a , A = 7 ah/2
octogone: n = 5 , P = 5 a , A = 8 ah/2
Exercice:
Calculer l'aire (blue) de la partie complémentaire au
pentagone par rapport au rectangle.
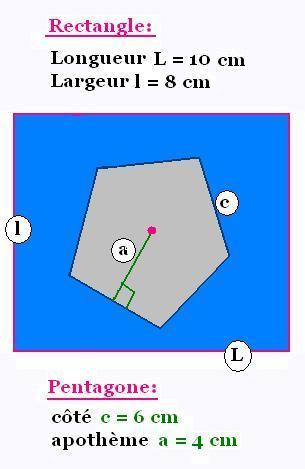
Réponse A = 20cm2.
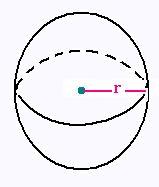
12. Sphère
r rayon de la sphère
Surface latérale S = 4πr2
Volume V:
V = (4/3)πr3
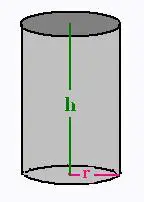
13. Cylindre
r rayon et h hauteur du cylindre
Surface latérale S = 2 π r2 + 2 π r h
Volume V:
V = π r2 x h
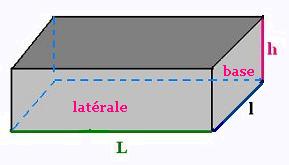
14. Prisme
r rayon et h hauteur du cylindre
Surface latérale S = 2 L x l + 2 L x h + 2 l x h
Volume V:
V = L x l x h
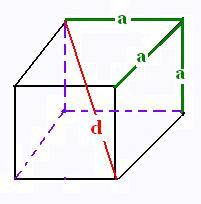
15. Cube
c côté du cube
Surface latérale S = 6 c2
Volume V:
V = c3
d2 = c2 + c2 + c2 = 3c2
Diagonale d = c √3
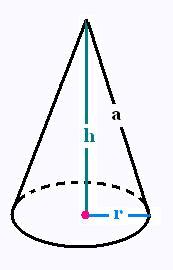
15. Cône
r rayon, h hauteur et a côté du cône
Surface latérale S = πr2 + πra
Volume V:
V = πr2h/3
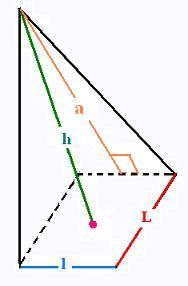
16. Pyramide
L logueur , l largeur h hauteur, a apothème de la pyramide
Surface latérale S = L x l + a (L + l)
Volume V:
V = L l h/3
|