Maths
- 2 -
Géométrie
© The scientific sentence. 2010
| |
| Mathématiques: Géométrie
Volume d'une pyramide régulière
Volume d'une pyramide tronquée
1. Pyramide et sections
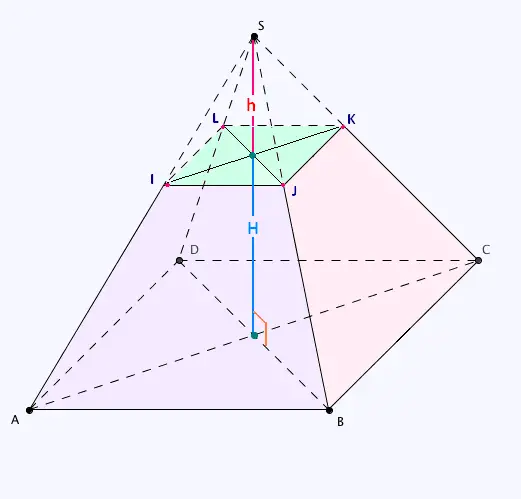
On considère une pyramide régulière SABCD à base carrée et de hauteur H + h.
On coupe cette pyramide, au niveau H à partir de sa base ABCD, suivant un plan
parallèle à cette base.
On obtient donc une section de cette pyramide qui est aussi un carré. ce carré
est une réduction du carré de base.
Cette transformation est une homothétie de centre l'apex S de la pyramide
et de rapport k tel que (segment image) = k (segment initial). C'est à dire:
h = k (h + H). h est la hauteur de nouvelle pyramide image réduite SIJKL.
Si la hauteur est réduite k , alors la surface de
base est réduite de k2, et le volume de
la pyramide image est k3 fois celui de la
pyramide initiale: SIJKL = k3 SABCD.
C'est une conséquence directe du théorème de Thalès.
Exemple:
H = 8 cm, h = 4 cm, et volume de la pyramide
initiale SABCD est de 324 cm3.
On réduit la payramide. Le rapport d'homothétie (ici le
coéfficient de réduction) est égal à k.
k = (hauteur image)/(hauteur initiale) =
4/(4 + 8) = 4/12 = 1/3.
Le volume de pyramide réduite image est donc (1/3)3 x 324 cm3
= 12 cm3.
2. Pyramide tronquée
Le volume de la pyramide tronquée (ou le tronc de la pyramide) est
la différence des volumes de la pyramide initiale
et celui de la pyramide finale: V(SABCD) - V(SIJKL).
On peut déterminer l'expression littérale du volume du tronc
de la pyramide:
Si Bg et Bp sont les bases respectives de la
grande pyramide (initiale) SABCD et de la petite pyramide (réduite)
SIJKL, on a:
V(SABCD) = Bg x (H + h)/3, et
V(SIJKL) = Bp x h/3.
D'autre part, selon les rapports de Thalès:
h/(h + H) = √Bp/√Bg.
D'où:
h = (√Bp/√Bg)H /(1 - √Bp/√Bg) =
H √Bp /(√Bg - √Bp)
Donc:
V(SABCD) - V(SIJKL) = Bg x (H + h)/3 - Bp x h/3 =
Bg x H/3 + (h/3)(Bg - Bp).
Calculons d'abord le produit h(Bg - Bp) :
h(Bg - Bp) = (√Bp H /(√Bg - √Bp))(Bg - Bp) =
(√Bp H)[(Bg - Bp)/(√Bg - √Bp)] =
(√Bp H)[√Bg + √Bp]
Il vient donc:
V(SABCD) - V(SIJKL) = Bg x H/3 + (1/3)(√Bp H)[√Bg + √Bp] =
(H/3)(Bg + Bp + √Bg√Bp)
Volume du tronc = (H/3)(Bg + Bp + √(BgBp))
Exemple:
H = 8 cm, base de la grande pyramide = 81 cm2, et
base de la petite pyramide = 9 cm2.
Volume de la pyramide tronquée = V(SABCD) - V(SIJKL) =
(8/3)(81 + 9 + √(81 x 9) = (8/3)(90 + 27) = 312 cm3.
3. Pyramide tronquée:
la méthode d'égypte antique

Énoncé du problème M14 du papyrus de Moscou.
Il s'agit d'une
méthode de calcul de volume d'une pyramide tronquée.
Si on te dit : Une pyramide de 6 pour la hauteur par 4 sur la base, par 2 sur le sommet. Calcule le carré de 4. Le résultat est 16. Prends le double de 4. Le résultat est 8. Prends le carré de 2. Le résultat est 4. Tu dois additionner le 16, le 8 et le 4. Le résultat est 28. Prends 1/3 de 6. Il vient 2. Prends 2 fois 28. Il vient 56. Le résultat est 56. Tu trouveras cela correct.
 Mathématiques égyptiennes
Mathématiques égyptiennes
|
|