Mathématiques 2: Symétrie et réflexion
La symétrie est une transformation géométrique.
Elle prends un objet et le transforme en son
image qui est une réplique exacte de l'objet.
Cette réplique est située sis à vis de l'objet
par rapport à un point ou par rapport à un axe.
1.Symétrie d'un point par rapport à un autre point
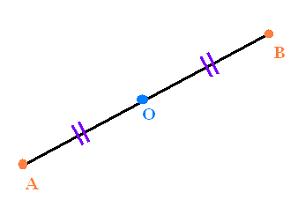 Le symétrique d'un point A par rapport à un
point O est le point B. Les points A et B sont
à égale distance du point O. C'est à dire:
[AO]=[OB]
Le point B est l'image du point A par symétrie.
Le symétrique d'un point A par rapport à un
point O est le point B. Les points A et B sont
à égale distance du point O. C'est à dire:
[AO]=[OB]
Le point B est l'image du point A par symétrie.
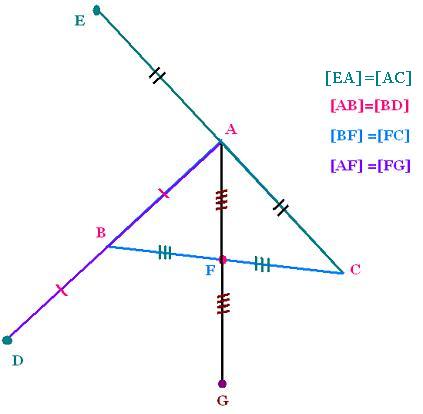
Exemple
E est le symétrique de C par rapport à A
D est le symétrique de A par rapport à B
B est le symétrique de C par rapport à F
G est le symétrique de A par rapport à F
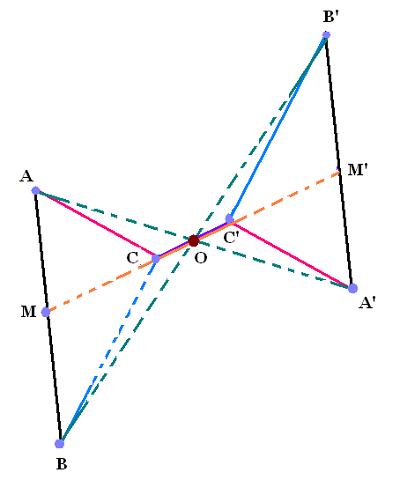
2. Symétrie d'une figure par rapport à un point
L'objet A'B'C' est l'image de l'object
ABC par symétrie.
Chaque point de la figure ABC est à égale distance de
son image de la figure A'B'C', par rapport au point O.
Le point O est appelé centre de symétrie et la symétrie
est dite centrale.
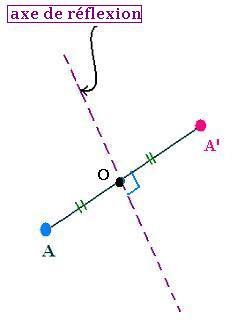
3. Symétrie d'un point par rapport à un axe de symétrie
Le symétrique d'un point A par rapport à un axe
de symétrie est le point A', image du point A.
Les points A et A' sont à égale distance de l'axe
de symétrie:
[AO] = [OB].
Le segment [AB] est perpendiculaire à l'axe de
symétrie (ou l'axe de réflexion).
4. Symétrie d'une figure par rapport à son axe de symétrie
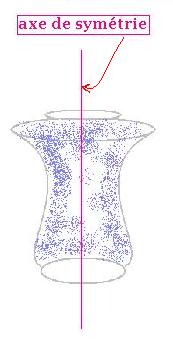
4.1. Symétrie axiale
Lorsque l'axe de symétrie coupe l'objet en
deux parties symétriques, la transformation est
appelé symétrie ou symétrie axiale.
4.2. Réflexion
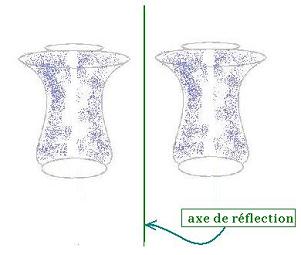
Lorsque l'axe de symétrie est exactement de part et
d'autre de l'objet et de son image, la transformation
est dite réflexion.
4.3. Cas général d'une réflexion
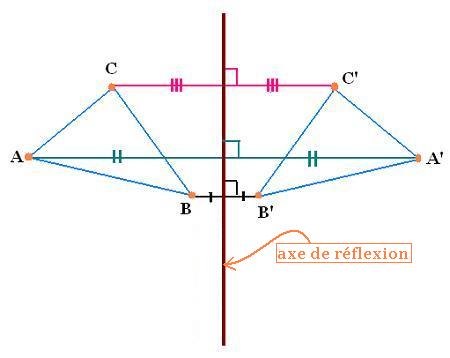
L'objet A'B'C' est l'image de l'object
ABC par symétrie axiale.
Chaque point de la figure ABC est à égale distance
de son image de la figure A'B'C', par rapport à
l'axe de symétrie.
Chaque segment de droite qui joint un point de
l'objet ABC à son image de l'objet A'B'C' est
perpendiculaire à l'axe de symétrie.

|