Mathématiques 2: Géométrie
Théorème des milieux

1. Énoncé du théorème

La droite qui passe par les milieux de deux côtés d'un triangle quelconque est parallèle au troisième côté.

La longueur du segment qui a pour extrémités les milieux de deux côtés d’un triangle quelconque est égale à la moitié de celle du troisième côté.

2. Démonstration du théorème

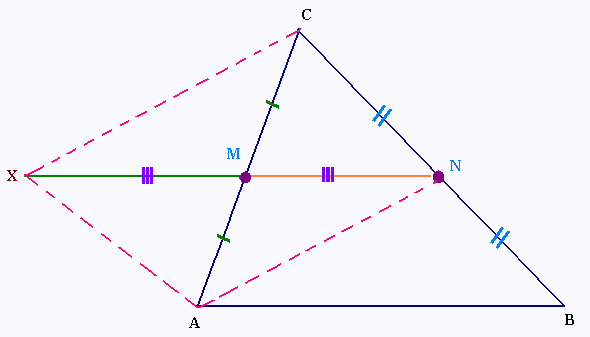
ABC est un triangle quelconque.
M est le milieu du segment [AC].
et N est le milieu du segment [BC].

On veut démontrer:

a) la droite (MN) est parallèle à (AB)
b) MN= AB/2

a) On construit un point auxiliaire X, symétrique de N par rapport à M, on a donc M milieu de [XN] et MN = XN/2

Par hypothèse M est le milieu de [AC], ainsi les diagonales du quadrilatère ANCX se coupent en leur milieu commun M, donc ANCX est un parallélogramme.

Et par conséquent les côtés [XC] et [AN] sont parallèles et de même longueur, et il en est donc de même pour les côtés [NC] et [AX].

Par hypothèse N est le milieu de [BC], ainsi CN = NB. Donc [BN] et [AX] sont parallèles et de même longueur.

Le quadrilatère ABNX n’est pas croisé.
On utilise la réciproque de la propriété du parallélogramme:

si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur alors c'est un parallélogramme.

Donc ABNX est un parallélogramme.

Par la définition du parallélogramme:

un parallélogramme est un quadrilatère dont les côtés opposés sont deux à deux parallèles ,

on en déduit que les côtés opposés [NX] et [AB] sont parallèles.

La droite (MN) est donc parallèle à (AB).

(MN) // (AB)

b) Selon la propriété du parallélogramme:

dans un parallélogramme, les côtés opposés ont même longueur,

on en déduit que XN = AB.

M est le milieu de [XN], donc MN = XN/2 = AB/2 .

MN = AB/2

3. Exercices

3.1. Exercice 1

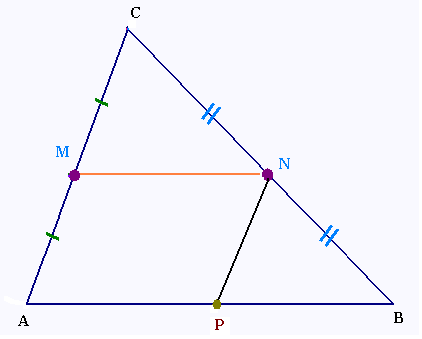
ABC est un triangle quelconque.
M est le milieu du segment [AC].
et N est le milieu du segment [BC].

On construit le point P milieu de [AB].

Montrer que le quadrilatère APNM est un parallélogramme.

Solution

Nous avons démontré que (MN) // (AB) et que MN = AB/2

P etant le milieu de [AB], donc AP = PB

On a onc (MN) // (AP) et MN = AP

On utilise la réciproque de la propriété du parallélogramme:

si un quadrilatère non croisé a deux côtés opposés parallèles et de même longueur alors c'est un parallélogramme.

Ainsi le quadrilatère MNPA est un parallélogramme.

3.2. Exercice 2

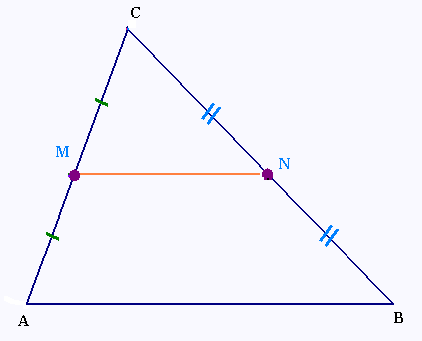ABC est un triangle quelconque.
M est le milieu du segment [AC].
et N est le milieu du segment [BC].

Utiliser le théorème de Thalès pour montrer que MN est la moitié de AB.

Solution

Le théorème de Thalès permet d'ecrire:

CM/CA = CN/CB = MN/AB

Par hypothèse, M est le milieu du segment [AC] et N est le milieu du segment [BC], on réécrit la formule de Thalès :

CM/CA = CN/CB = MN/AB= 1/2

Ainsi

MN = AB/2