Maths
- 2 -
Géométrie
© The scientific sentence. 2010
| |
|
Mathématiques: Géométrie
Triangle rectangle et cercle circonscrit
1. Cercle circonscrit à un triangle rectangle:
1. Diamètre du cercle circonscrit:
Propriété 1:
|
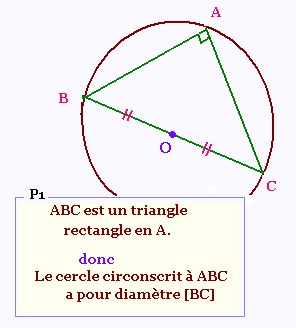
Si un triangle est rectangle, alors son
cercle circonscrit a pour diamètre
l'hypoténuse.
Ou bien, le
cercle circonscrit à un triangle rectangle
a pour centre le milieu de son
hypoténuse.
Cette propriété peut permettre de démontrer que
trois points appartiennent à un même cercle.
|
2. Conséquences
Propriété 2:
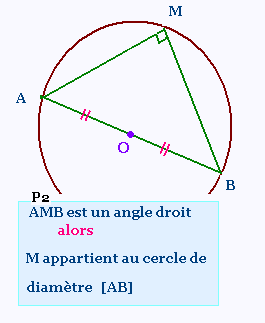
Si AMB est un angle droit, alors le point M appartient
au cercle de diamètre [AB].
|
|
Propriété 3:
|
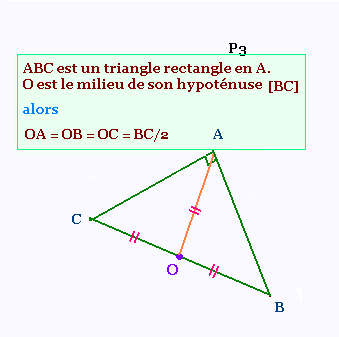
Si un triangle est rectangle, alors
la longeur de la médiane relative à l'hypoténuse est égale
à la moitié de la longeur de l'hypoténuse.
Ou bien, dans un triangle rectangle,
le milieu de l'hypoténuse est équidistant des trois
sommets.
Cette propriété peut permettre de démontrer que
des longeurs sont égales.
|
2. Les réciproques
Réciproque de la propriété 1:
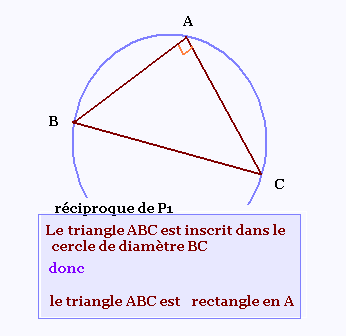
Si un triangle est inscrit dans un cercle de diamètre l'un
de ses côtés, alors ce triangle est
rectangle.
Cette propriété peut permettre de démontrer qu'un
triangle est rectangle.
|
|
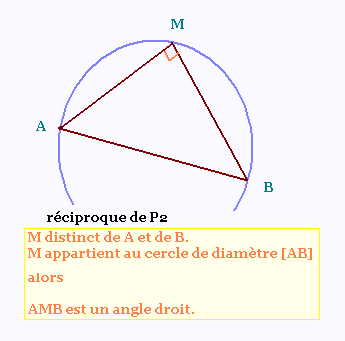
Réciproque de la propriété 2:
|
Si un point M, distinct de A et de B appartient au
cercle de diamètre [AB], alors AMB est un angle droit.
Cette propriété peut permettre de démontrer qu'un
angle est droit.
|
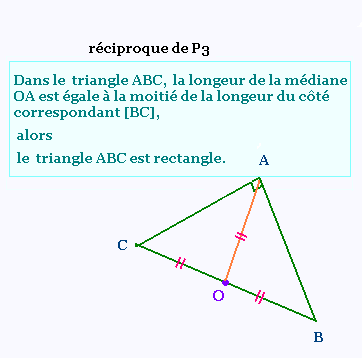
Réciproque de la propriété 3:
Si dans un triangle la longeur d'une la médiane est égale à
la moitié de la longeur du côté
correspondant, alors ce triangle est rectangle.
Cette propriété peut permettre de démontrer qu'un
triangle est rectangle.
|
|
3. Exercice:
Tangentes à un cercle passant par un point donné
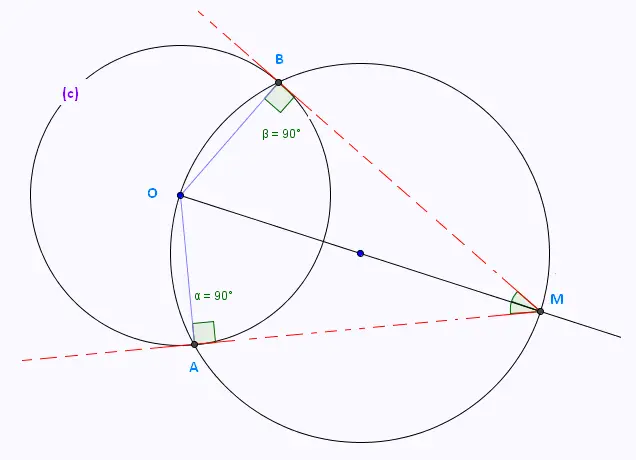
Étant donné un cercle (c) de centre O et un point M à l'extérieur du cercle,
les points de contact A et B des tangentes issues de M sont les points
d'intersection du cercle (c) et du cercle de diamètre [OM].
Montrer que [OM] est la bissectrive de l'angle et
la médiatrice du segment [AB].
|
|