Mathématiques 2: Géométrie
Les graphes
Termes et définitions
Exercies

1. Le graphe

Des deux graphes suivants, donner un exemple de chacune des définitions énumérées ci-dessous :



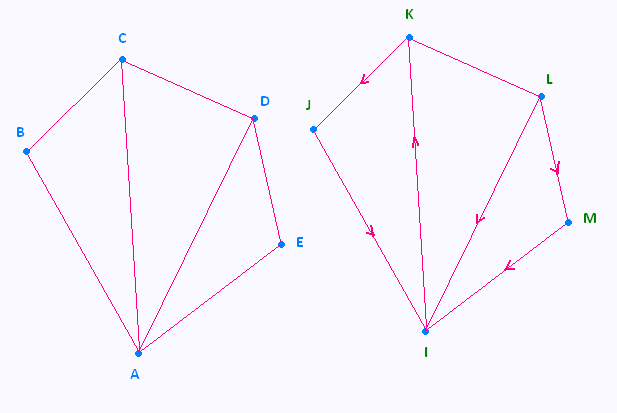
• Arc : Trait ou courbe avec une flèche (orienté) reliant deux sommets.

• Arête : Trait ou courbe (non-orienté) reliant deux sommets.

• Degré d’un sommet : Nombre d'arêtes (ou un arcs) sur un sommet.

• Graphe : Représentation géométrique d'un ensemble contenant des sommets reliés par des arêtes ou des arcs.

• Ordre d'un graphe: Nombre de sommets qu'il contient.

• Graphe orienté : Graphe utilisant des arcs au lieu des arêtes.

• Graphe valué : Graphe construit avec des arêtes contenant des valeurs.

• Sommet :Point relié par des arcs ou des arêtes.

2. Propriétés des geaphes

Des deux graphes suivants, donner un exemple de chacune des propriétés énumérées ci-dessous :

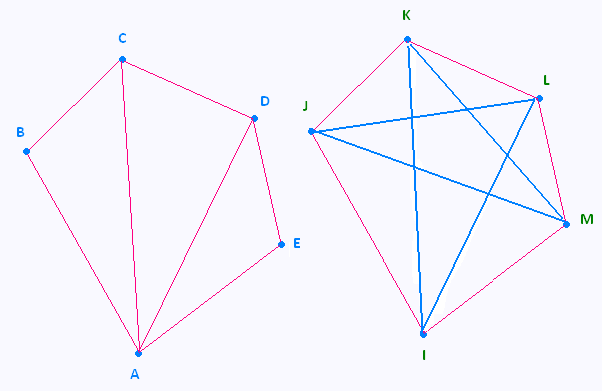
1. Graphe non-orienté

• Chaîne : Ensemble de sommets reliés par des arêtes entre eux de façon continue.

• Chaîne Simple : Une chaîne qui n'utilise jamais deux fois la même arête.

• Chaîne Eulérienne : Chaîne simple qui passe par toutes les arêtes d'un graphe. Le graphe doit contenir exactement deux sommets de degré impair.

• Chaîne Hamiltonienne : Chaîne simple qui passe par tous les sommets d'un graphe une et une seule fois.

• Cycle : Un cycle est une chaîne qui revient à son point de départ.

• Cycle simple : C’est un cycle dont toutes les arêtes du cycle sont utilisées une et une seule fois.

• Cycle Eulérien : Cycle simple qui passe par toutes les arêtes d'un graphe. Tous les sommets du graphe doivent être de degré pair.

• Cycle Hamiltonien : Cycle simple qui passe par tous les sommets du graphe une et une seule fois.

2. Graphe orienté

• Chemin : Les sommets sont reliés par des arcs de façon continue.

• Circuit : Un circuit est un chemin qui revient à son point de départ.