Mathématiques 2: Théorème de Thalès
1. Thalès et les rapports de similitude
Thalès de Milet (-625, -547) était un mathématicien de la Grèce antique. La légende dit qu'il fut le premier à réussir à calculer la hauteur de la grande pyramide de Khéops en utilisant les rapports de similitude de deux triangles semblables.
Pour cela, Il planta une tige de longeur connue verticalement
dans le sol et mesure son ombre. Ensuite, il mesura l'ombre de la Pyramide. Il trouva alors une valeur de 134 Thalès pour la hauteur de la pyramide (Un Thalès correspond à la taille de Thalès soit 1,73 m).
2. Théorème de Thalès
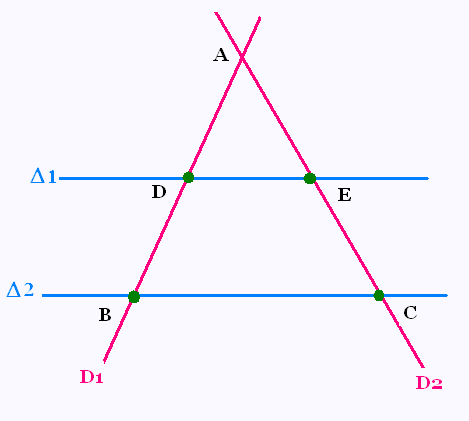
Soit deux droites parallèles Δ1 et Δ2
coupées par deux droites sécantes
D1 et D2.
Ces quatre droites forment deux triangles :
• Le grand triangle ABC et
• Le petit triangle ADE.
L'angle B est isométriques à l'angle D, comme angles
correspondants. De même pour les angles C et E.
Donc ces deux triangles ont leurs côtés
proportionnels. Ils sont donc semblables.
Leur rapport de similitude est égale à
AB/AD = AC/AE = BC/DE = k .
Ainsi
Ceci démontre le théorème de Thalès.
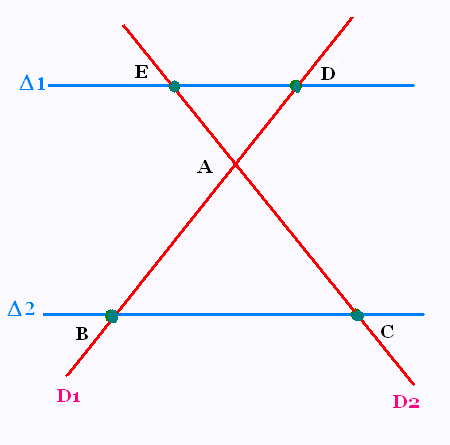
Le théorème de Thalès se démontre et
s'applique aussi bien quand les sécantes se croisent
à l'exterieur des droites parallèles qu'à l'intérieur.
On note que le théorème de Thalès est juste une manière d'ecrire
les rapports de similitude de deux triangles semblables.
3. Autres versions de la propriété de Thalès
Théorème de Thalès
Étant donné un triangle ABC,
si D est un point du côté [AB]
et si E est un point du côté [AC]
tels que (MN) et (BC) sont parallèles,
alors : AD/ AB = AE/AC = DE/BC
Théorème de Thalès
Étant donné deux droites (D1) et (D2)
sécantes en A,
deux points D et B de (D1) distincts de A,
deux points E et C de (D2) distincts de A,
si les droites (BC) et (DE) sont parallèles ,
alors : AD/ AB = AE/AC = DE/BC
Démonstration du théorème de Thalès
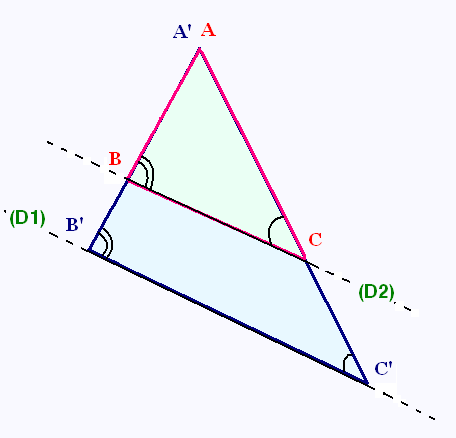
La démonstration suivante utilise la première
figure où le point A est extérieur aux droites parallèles.
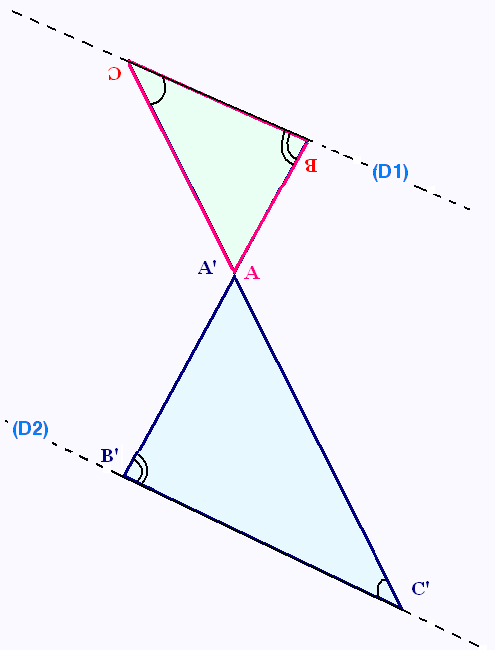
(la démonstration est similaire avec la figure 2
où le point A est intérieur aux droites parallèles:
ici les angles congrus sont alternes internes plutôt
que correspondants comme dans la figure 1).
Étant donné un triangle A'B'C',
B est un point du côté [A'B']
C est un point du côté [A'C']
Si (BC) et (B'C') sont parallèles, alors les angles
correspondants ∠B et ∠ sont égaux
Ainsi, selon le critère AA des triangles semblables, les
triangles ΔABC et ΔA'B'C' sont semblables.
d'où: AD/ AB = AE/AC = DE/BC.
Réciproque du théorème de Thalès
Étant donné deux droites (D1) et (D2)
sécantes en A,
deux points D et B de (D1) distincts de A,
deux points E et C de (D2) distincts de A,
si dans l'ordre ADB-AEC, on AD/ AB = AE/AC ,
alors : les droites (BC) et (DE) sont parallèles .
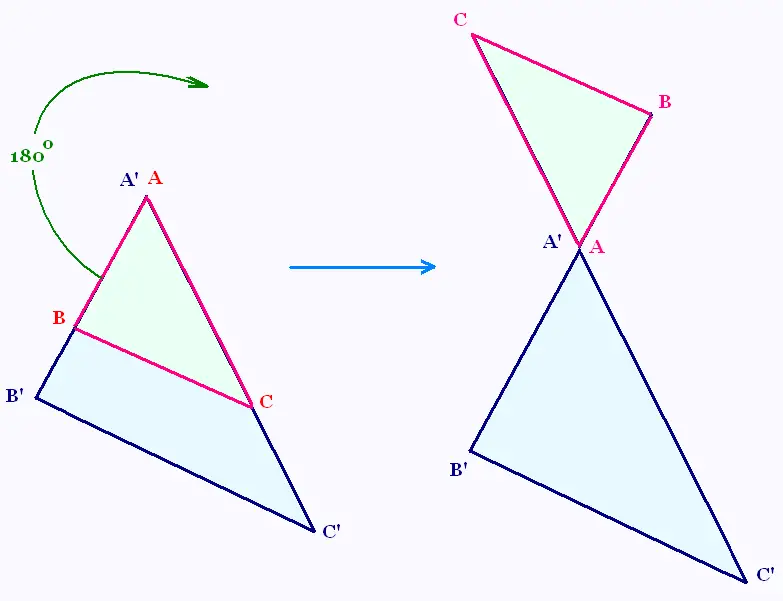
3. Positions des triangles dans la propriété de Thalès
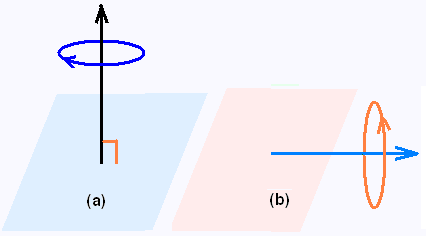
Les sécantes se croisent à l'extérieur des droites parallèles
ou à l'intérieur.
On passe d'une disposition à l'autre soit par symetrie centrale autour
du point A = rotation de 180° autour du point A (figure a), soit par symetrie axiale autour d'un axe parallèle au côté opposé à
l'angle A (figure b).
C'est la première disposition qui est la plus utilisée:
 4. Applications
|
