Mathématiques: Algèbre
Calcul littéral

1. Définitions

L'Arithmétique est la science des nombres. On étudie juste des nombres. On cherche les résultats des opérations numériques des nombres donnés.

Faire la somme de deux nombres ou calculer leur pgcd est arithmétique.

L'Algèbre généralise l'Arithmétique. Elle résoud les équations en cherchant les inconnus.

Résoudre une équation du second degré est algébrique. l'algèbre utilise le calcul numérique, mais surtout le calcul littéral.

Le calcul littéral utilise des lettres qui représentent des nombres inconnus.

Voici une expression littérale: x² - 2x + 5.

Le calcul littéral est souvent une transformation de

• Réduction,
• Développement, ou son inverse,
• Factorisation.

Réduire une expression littérale, c'est rassembler ce qui se ressemble.

2x - 3 + 7 + 5x = 2x + 5x - 3 + 7 = 7x + 4 .

Développer une expression littérale, c'est défaire les factorisations de cette expression. On utilise une simple distributivité, ou une double distributivité, ou plusieurs distributivités.

(x - 1)(x + 2) = x² + x - 2 .

Factoriser une expression littérale, c'est mettre cette epression sous formede facteurs. C'est la transformation inverse du développement.:

x² + x - 2 = (x - 1)(x + 2)

2. Identités remarquables

Les identités remarquables sont utilisées dans le calcul algébrique littéral. Elles permettent de simplifier l'ecriture des expressions et d'aller plus vite dans les transformations réduction ↔ factorisation.

Les plus utilisées et à savoir par coeur sont:

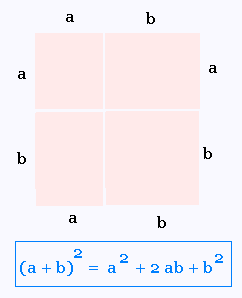
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
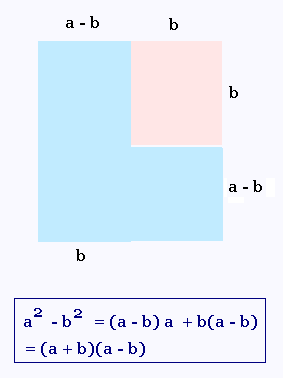
a² - b² = (a + b)(a - b)

(a + b)³ = a³ + 3 a² b + 3 ab² + b³
(a - b)³ = a³ - 3 a² b + 3 ab² - b³
a³ - b³ = (a - b )(a² + ab + b²)
a³ + b³ = (a + b )(a² - ab + b²)

(a + b + c)² =
a² + b² + c² + 2ab + 2ac + 2bc

les lettres a, b, c ... représentent n'importe quel nombre ou expression algébrique.

À l'origine, les identités remarquables ont été géométriques. Par l'Algèbre, en utilisant le binôme de Newton, on peut les étendre à n'importe quelle puissance.