Mathématiques 2: Les échelles
1. Définitions
Un objet a des dimemsions réelles. On note les
valeures de ces dimensions sur un papier.
Les dimensions du papier que l'on utilse ne sont ni
des millimètres (mm) ni des kilomètres (km), juste
des centimètres.
On peut donc transcrire sur ce papier l'objet de
n'importe quelle dimemsion au moyen d'un
agrandissement ou d'une réduction.
La procédure utilisée pour ces opérations est
appelée reproduction à l'échelle.

2. Example: réduction
Le Rayon moyen de la terre est de 6 371.00 km. On
représente la terre sur un plan de papier.
On prendra 2000.00 km dans le terrain (dans la
réalité) pour 1 cm sur papier.
Si 2000.00 km → 1 cm , alors
1 km → (1/2000) cm , donc
6371.00 km → 6371.00 x (1/2000) cm = 3.185 cm =
3.19 cm au 100ième près.
 Il s'agit d'une réduction.
L'échelle tilisée est de: 1 cm/2000 km .
En convertissant aux mêmes unités, on obtient:
1 cm/2000 km = 1 cm/200 000 000 cm = 1/200 000 000.
Échelle = 1/200 000 000 ou 1:200 000 000.
Une échelle de n:m signifie que n unités
sur le dessin (papier) représentent m même unités
dans la réalité (sur le terrain).
Il s'agit d'une réduction.
L'échelle tilisée est de: 1 cm/2000 km .
En convertissant aux mêmes unités, on obtient:
1 cm/2000 km = 1 cm/200 000 000 cm = 1/200 000 000.
Échelle = 1/200 000 000 ou 1:200 000 000.
Une échelle de n:m signifie que n unités
sur le dessin (papier) représentent m même unités
dans la réalité (sur le terrain).
3. Example: agrandissement
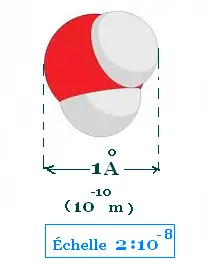
La dimension moyenne d'une molécule d'eau est d'un
Angstrom, c'est à dire le dixième du milliardième
du mètre.
1 Angstrom (Å) = 10- 10 m.
Si on veut représenter les dimensions de la molécule
sur papier, il faut faire un agrandissement.
On doit donc avoir une échelle n:m avec n > m.
Nous prenons l'échelle comme suit
2 cm sur le dessin représentera 1 Å dans la
réalité.
Donc:
2 cm → 10- 10 m, soit une échelle de 2 cm /10- 10 m.
En convertissant aux mêmes unités, on obtient:
2 cm /10- 10 m = 0.02 m /10- 10 m = 2 /10- 8.
Échelle = 2 /10- 8 ou 2:10- 8
(un agrandissement de 200 millions de fois)
3. Exercices
3.1. Exercice 1: carte routière
Voici une carte routière.
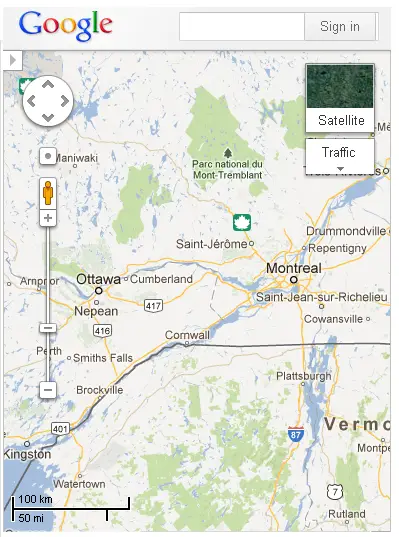
Estimer la distance entre Montréal et Ottawa.
On peut utiliser une règle graduée.
3.2. Exercice 2: Honda Odyssey 2004
 Une automobile Honda Odyssey mesure 201.2 pouces
de longeur et 75.6 pouces de hauteur. Quelle
sont ces dimensions en cm sur un papier avec
une échelle de 1:100?
Une automobile Honda Odyssey mesure 201.2 pouces
de longeur et 75.6 pouces de hauteur. Quelle
sont ces dimensions en cm sur un papier avec
une échelle de 1:100?
1 pouce = 2.54 cm.
3.3. Exercice 3: Siège social des Nations Unis

Le siège social des Nations Unis à New York
est un bâtiment de 168 mètres de hauteur.
À quelle
échelle est représentée cette hauteur sur la photo?
3.4. Exercice 4: La Tour de la Paix

La Tour de la Paix, est située au centre
du Parlement du Canada, à Ottawa, en Ontario.
Sa hauteur est de 99.0 mètres.
Sur un plan, comme dans la photo, cette hauteur
mesure 4.3 cm.
Quelle est l’échelle de cette photo?
3.5. Exercice 5: Tableau de mesures
Compléter le tableau suivant.
La dernière échelle est fausse dites pourquoi.
Mesure sur
le papier (cm) |
Mesure sur
le terrain |
Échelle |
| 12 | 60 m | ... |
| ... | 15 km | 1:750 000 |
| 10 | 0.1 mm | ... |
| 20 | ... | 4:10 000 000 |
| 3 | 0.03 mm | ... |
| 12 | ... | 100:1 |
| ... | 240 mm | 1:1 |
| 15 | 150 mm | ... |
| 6 | ... | 1:100 |
| ... | 60 m | 2:300 |
| 24 | ... | 3:50 000 000 |
| ... | 80 m | 5:10 |
3.6. Exercice 6: Distance terre-lune
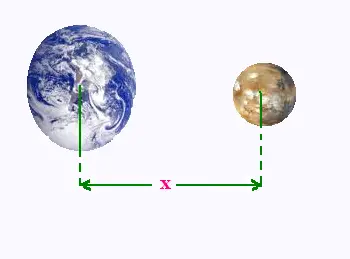
Sur cette image la distance terre-lune est
représentée par 6.5 cm, avec une échelle de
17:100 000 000 000. Quelle est
la distance réelle entre la terre et la lune?
3.7. Surface d'un polygone
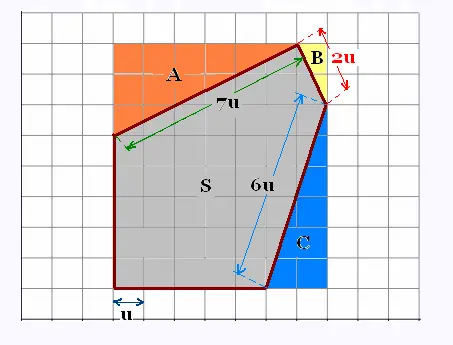
Un pentagone non régulier est déssiné sur un
papier. Une unité sur le papier représente
1cm. Le périmètre du pentagone sur le terrain est
de 200 mètres.
Calculer l'aire réelle du pentagone.
Solutions
|