Mathématiques 45: Algèbre:
Fonction quadratique
Fonction quadratique
1. Forme générale
La forme générale d'une fonction
quadratique est
f(x) = ax2 + bx + c
La courbe d'une fonction quadratique
est une parabole.
2. Orientation de la parabole:
Si a > 0, la parabole sera ouverte vers le haut
Si a < 0, la parabole sera ouverte vers le bas
2. Les zéros de la fonction:
L'équation ax2 + bx + c = 0 a :
Deux solutions distinctes si Δ > 0:
x1 = (- b + √Δ)/2a , et
x2 = (- b + √Δ)/2a
Une solution double si Δ = 0:
x12 = - b/2a
Aucune solution si Δ < 0:
x12 = - b/2a
Avec
Δ = b2 - 4ac.
3. Sommet de la parabole:
Le sommet de la parabole = (h, k) avec
h = - b/2a, et
k = (4ac - b2)/4a
3. Forme canonique de la fonction quadratique:
Avec
h = - b/2a, et
k = (4ac - b2)/4a,
la forme générale ax2 + bx + c devient:
f(x) = a(x - h)2 + k
C'est la forme canonique de la fonction
quadratique.
4. Signification des paramètres h et k
. Le paramètre h traduit une translation horizontale
selon l'axe des x:
si h > 0, la translation se fait vers la droite de h unités.
si h < 0, la translation se fait vers la gauche de h unités.
. Le paramètre k traduit une translation verticale
selon l'axe des y:
si k > 0, la translation se fait vers le haut de k unités.
si k < 0, la ranslationse fait vers le bas de k unités.
5. Exemple:
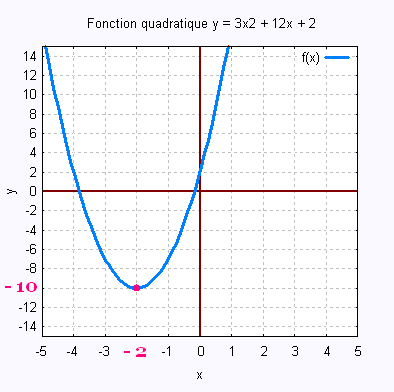
Soit le trinôme : 3x2 + 12x + 2
Il possède deux racines distinctes :
- 3.83 et - 0.17
Sous forme factorisée, il s'ecrit donc :
3(x + 3.83)(x + 0.17)
Sous forme canonique:
h = - b/2a = - 12/(2x3) = - 2 et
k = - 122/(4x3) + 2 = - 12 + 2 = - 10.
Donc:
3x2 + 12x + 2 = 3(x + 2)2 - 10
.
|