Mathématiques 2: Fonctions
Fonctions élémentaires
1. Définitions
On rappelle qu'une variable indépendante est une variable
qui varie d'elle même, mais la variable dépendante varie
juste parce que la variable dont elle dépends varie.
Exemple:
Le temps passe: variable indépendante.
La population mondiale augmente: variable dépendante
Elle augmente au fur et à mesure que le temps passe.
La variable dépendante est fonction de la variable
indépendante. Elles sont donc liées par une équation
.
Si x est la variable indépendante, et
y la variable dépendante correspondante (elle varie en
fonction de x), fonction de x, alors, on peut
ecrire:
y = ƒ(x)
Exemple: Population y est fonction du temps x:
y = ƒ(x)
Nous allons étudier les fontions les plus simples. Elles
sont de type:
y = b
y = a x
y = a x + b
y = a/x
a et b sont des paramètres constants.
2. Exemples
2.1. Fonction constante : y = b
On s'interesse à la vitesse de la lumière (dans le vide).
Soit x la variable indépendante temps,
y est la variable dépendante vitesse associée.
On sait que cette vitesse vaut 300 000 km/s.
Elle est constante tout le temps. On représente
donc la variable vitesse par y et la variable temps
par x et on ecrit:
y = ƒ(x) = a = 300 000.
y ne dépends pas de x
La représentation graphique de
cette fonction est la suivante:
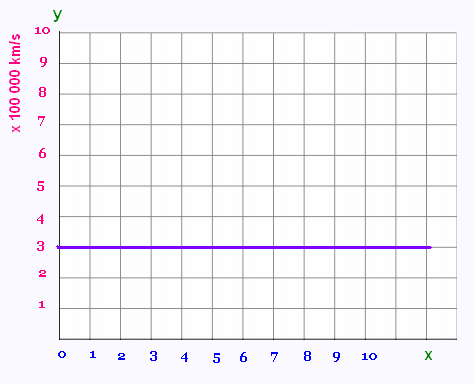
C’est une droite parallèle à l’axe des x.
2.2. Fonction linéaire y = a x
On s'interesse à la distance parcourue par
un coureur, à vitesse constante v = 10 km/h.
La distance qu'il parcourt est fonction du temps.
Soit x la variable indépendante temps,
y est la variable dépendante distance associée.
On représente la variable distance par y et la variable temps
par x et on ecrit:
y = ƒ(x) = v x
x en heures ey y en km.
y dépends linéairement de x
La représentation graphique de
cette fonction est la suivante:
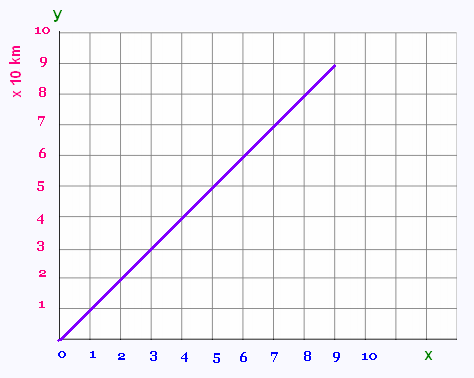
C’est une droite oblique passant par l'origine.
2.3. Fonction affine y = a x + b
On s'interesse au prix à payer pour louer une
voiture pour une journée.
Le prix de location est de 20$ auquel il faut
ajouter 10 ¢ pour chaque kilomètre effectué.
Le prix de location est fonction du kilomètre effectué.
Soit x la variable indépendante kilomètre effectué,
y est la variable dépendante prix de location associée.
On représente la variable prix de location par y et la
variable kilomètre effectué par x et on ecrit:
y = ƒ(x) = 0.1 x + 20 en $
y dépends linéairement de x
La représentation graphique de
cette fonction est la suivante:
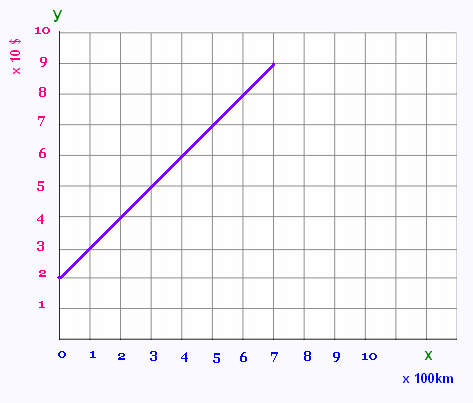
C’est une droite oblique ne passant pas par
l’origine. Elle passe par le point (0,b) où b = 20.
2.4. Fonction rationnelle y = a/x
On veut partager 1000 $ à 10 élèves dans un Math-Idol.
La somme distribuée est fonction du nombre d'élèves reçus.
Soit x la variable indépendante nombre d'élèves reçus,
y est la variable dépendante somme distribuée associée.
On représente la variable "somme distribuée" par y et
la variable "nombre d'élèves reçus" par x et on ecrit:
y = ƒ(x) = 1000/x
y dépends linéairement de x
La représentation graphique de
cette fonction est la suivante:
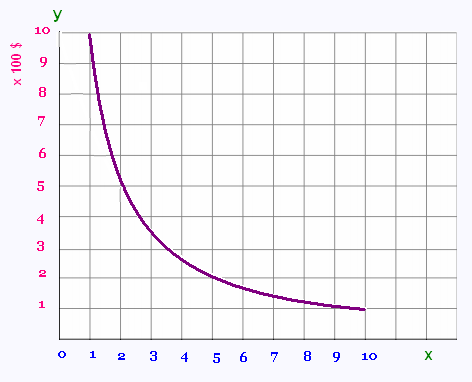
C’est une courbe dite hyperbole dont les extrémités se rapprochent des 2 axes.
|