Maths
- 2 -
© The scientific sentence. 2010
| |
|
Mathématiques 2: Polygones avec Geogebra
1. Somme des angles extérieurs des polygones
1.1. Polygones réguliers
1. Ouvrire GeoGebra en cliquant sur le bouton:
2. Utiliser une page vierge (sans axes et sans grille)
3. À l’aide de l’outil Polygone régulier:
tracer des polygones réguliers à 3, 4, 5, 6, 7 et 8 côtés.
4. Pour chacun des polygones, identifie la mesure d’un angle
intérieur et la mesure de l’angle extérieur correspondant.
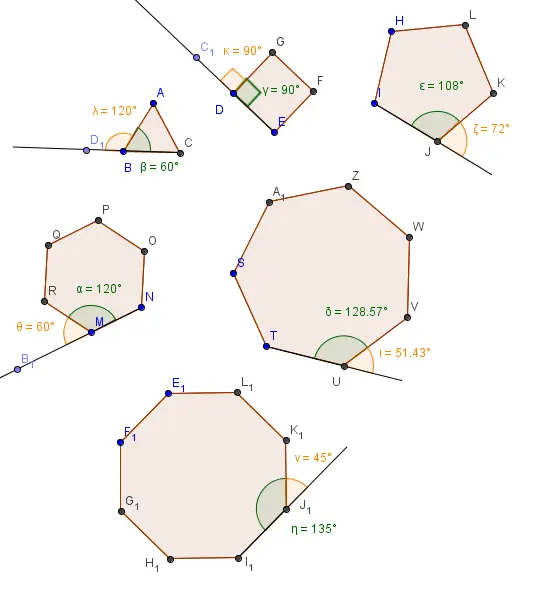
Dans un polygone régulier, tous les angles intérieurs sont congrus.
Leur somme est égale à (n - 2) x 180° où n est le nombre
de côtés du polygone.
Chaque angle intérieur du polygone mesure donc
(n - 2) x 180°/n.
L'angle extérieur associé mesure donc
180° - (n - 2) x 180°/n =
2 x 180°/n = 360°/n
Donc la somme des mesures des n angles extérieurs est
n x 360°/n = 360°
La somme des mesures des angles extérieurs d'un plygone
régulier est égale à 360°
.
1.2. Polygones irréguliers
La somme des mesures des angles intérieurs d'un
polygone non régulier est égale aussi à (n - 2) x 180°,
comme pour un polygone régulier. Mais ces angles intérieurs
ne sont pas congrus.
La somme des mesures des angles extérieurs d'un
polygone non régulier est égale aussi à 360°,
comme pour un polygone régulier. Mais ces angles extérieurs
ne sont pas congrus.
Exemple: Heptagone non régulier:
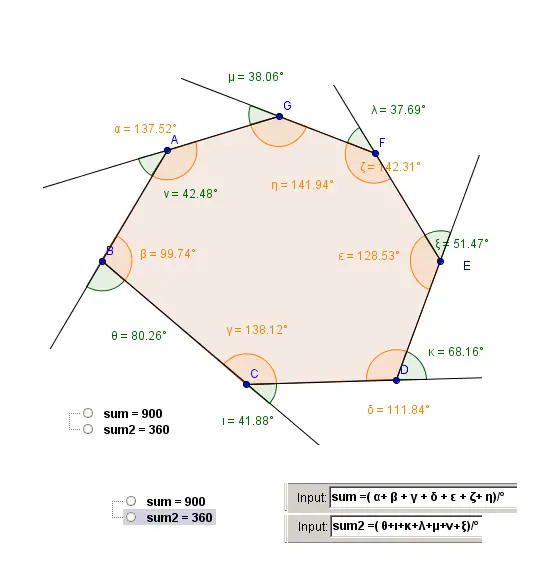
2. Somme des angles extérieurs et
intérieurs d'un polygone concave
Les résultats relatifs à un plygone convexe , que ce soit
régulier ou non, restent valable pour un polygone concave
régulier ou non.
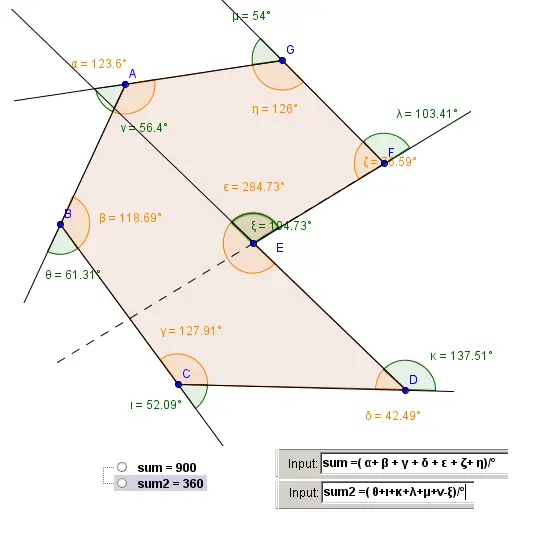
Exemple: Heptagone concave non régulier
|
|