Mathématiques 45: Géométrie:
Pente d'une droite dans le plan cartésien

1. Pente d'une droite

L'équation d'une droite, ecrite sous sa forme fonctionnelle est: y = ax + b

a: est appelé la la pente ou le taux de variation.
b : valeur initiale ou l’ordonnée à l’origine.

La pente d'une droite détermine la valeur de son l’inclinaison par rapport à l’horizontale.

Si la pente est positive (a > 0), la droite est croissante,

Si la pente est négative (a < 0), la droite est décroissante.

2. Calcul de la pente

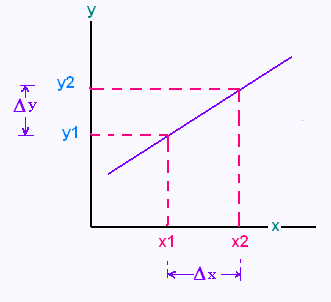
Si y1 est la valeur de la variable dépendante correspondante à la valeur x1 de la variable indépendante, et
y2 la valeur de la variable dépendante correspondante à la valeur x2 de la variable indépendante, on note Δy = y2 - y1 la variation de y et Δx = x2 - x1 celle de x.

On ecrit ainsi la sous l'expression:

a = Δy/Δx = (y2 - y1)/(x2 - x1)

La pente d'une droite est égale à la variation des y sur la variation des x.

On le calcule selon la méthode de comparaison:

y1 = a x1 + b
y2 = a x2 + b

donc y2 - y1 = a(x2 - x1)

d'où:

a = (y2 - y1)/(x2 - x1)

3. Exemple

3.1. Exemple 1

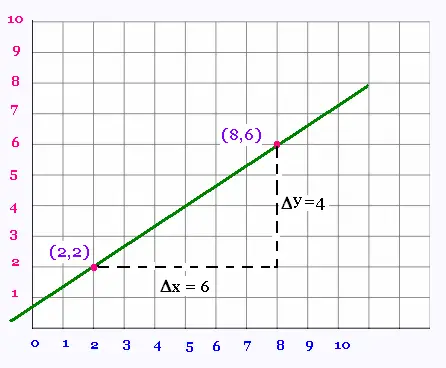
Quelle est la pente de la droite définie par son graphe suivant:

a = Δy/Δx = 4/6 = 0.67

3.2. Exemple 2

Quelle est la pente de la droite qui passe par les points P1(- 3, +4) et P2(+2, -5) ?

a = Δy/Δx = (- 5 - 4)/(2 + 3) = - 9/5 = - 1.8

3.3. Exemple 3

Quelle est la pente de la droite d'équation y = - 5 ?

Cette droite est parallèle à l'axe des x. Elle est constante. Sa pente est nulle.

a = Δy/Δx = (- 5 + 5 )/(x2 - x1) = 0

x1 et x2 sont deux abscisses quelconques.

3.4. Exemple 4

Quelle est la pente de la droite d'équation x = + 3 ?

Cette droite est parallèle à l'axe des y. Elle est constante. Sa pente est indétérminée.

a = Δy/Δx = (y2 - y1 )/(3 - 3) : indétérminée.

y1 et y2 sont deux ordonnées quelconques.

3.5. Exemple 5

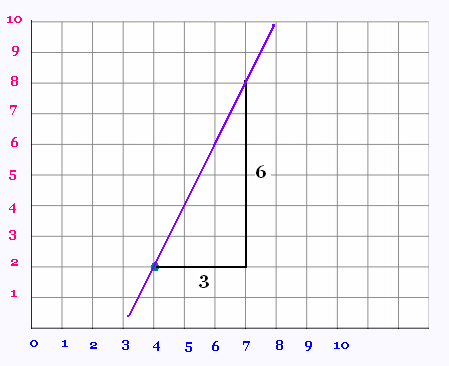
Tracer la droite de pente égale à + 2 et passant par le point P1(4,2).

À partir du point P1, on prend un Δx = 3 et un Δy = 6 pour avoir une pente de 2. On obtient le point P1.

On joint les points P1P2. Ce qui constitue la droite cherchée.

On pourrait prendre Δx = 1 et Δy = 2. L'essentiel c'est d'avoir le rapport 3.