Mathématiques 2: Geométrie: Les Perspectives:
Les projections parallèles et centrales
Résumé
projection parallèle
Dans la perspectice cavalière, on commence par dessiner
une FACE frontale et on respecte le parallélisme. L'angle de fuite est 45°.
Le coefficient k de réduction des fuyantes varie de 0.5 à 0.7
(0 < k < 1).
Dans la perspectice axonométrique (isométrique), on commence par dessiner
une ARÊTE et on respecte le parallélisme . L'angle de fuite est 30°.
Le coefficient des réduction des fuyantes est égal à 1.
projection centrale
Dans la perspectice centrale ou conique à un point de fuite, on commence par dessiner
une FACE frontale et on respecte l'éloignement. L'angle de fuite et
Le coefficient de réduction des fuyantes dépend de la construction géométrique.
Dans la >perspectice à deux points de fuite, on commence par dessiner
une ARÊTE et on respecte l'éloignement. L'angle de fuite et
Le coefficient de réduction des fuyantes dépend de la construction géométrique.
Coefficient de réduction = (arête fuyante)/(arête réelle ou réduite à l'echelle).
1. La perspective
Une perspective est la façon de représenter
un objet en trois dimensions sur un plan.
La perspective est l'oeuvre d'un observateur. Elle
doit donc inclure la position de l'objet dans l'espace
par rapport à cet observateur, ainsi que l'effet de
l'éloignement.
L'effet de l'éloignement n'est pas réel, mais visuel.
Dans une projection parallèle, c'est à dire dans une perspective
cavalière ou axonométrique, on respecte le parallélisme.
Dans une projection centrale (conique), c'est à dire dans une perspective
à un point de fuite ou à deux points de fuite, on respecte plutôt
l'éloignement.
2. Les projections
La perspective est un type de projection .
Les projections sont parallèles ou centrales, ou
orthogonales.
La projection parallèle contient la perspective cavalière
et la perspective axonométrique.
La projection centrale contient la perspective à un point
de fuite et la perspective à deux points de fuite.
2.1. Les projections parallèles
Les projections parallèles sont des projections d’un objet
3D sur un plan qui conservent les droites parallèles.
C'est à dire les droites qui sont parallèles dans l’espace
restent parallèles sur le plan.
Les mesures des angles et des longueurs ne sont
pas conservées.
2.1.1. La perspective cavalière
On la construit de la façon suivante:
. 1. Dessiner UNE FACE de l’objet sur le plan.
2. Construire les arêtes obliques à partir des sommets de cette face,
. Les arêtes (les fuyantes) doivent être parallèles entre elles et
avoir un angle de profondeur d’environ 45 degrés.
. Le coefficient de réduction est égal à 0.7.
2.1.2. La perspective axonométrique
On la construit de la façon suivante:
1. Dessiner UNE ARÊTE de l’objet sur le plan,
2. Construire les fuyantes à partir des deux extrémités
de cette arête,
Les fuyantes qui se trouvent de même côté du segment
doivent être parallèles entre elles.
. L’angle de profondeur (de fuite) d’environ 30 degrés.
. Le coefficient de réduction est égal à 1.0.
2.2. Les projections centrales
Une projection centrale fournit une image plane d'un objet
tridimensionnel avec un effet visuel qui donne un effet de profondeur
La projection centrale conserve l'alignement et l'intersection,
mais ne conserve ni le parallélisme ni les rapports de distance.
Les projections centrales font l'objet d'une perspective à un point
de fuite ou perspective à deux points de fuite.
2.2.1. Perspective à un point de fuite
On la costruit de la façon suivante:
1. Dessiner UNE FACE de l’objet sur le plan,
2. Construire les fuyantes à partir des sommets de cette
face en les reliant au point de fuite.
Les arêtes horizontales et les arêtes verticales sont parallèles entre elles.
L'angle de fuite et le coefficient de réduction
dépendent de la construction.
.
2.2.2. Perspective à deux points de fuite
On la construit de la façon suivante:
1. Dessiner une ARÊTE verticcale de l’objet sur le plan,
2. Construire les fuyantes à partir des extrémités de cette arête
en les joignat aux points de fuite.
Seulement les arêtes verticales sont parallèles entre elles.
L'angle de fuite et le coefficient de réduction
dépendent de la construction.
3. Exemples:
Les longeurs des côtés a, b, c, ...
sont réelles dans l'espace ou, réduites à l'échelle.
3.1. Exemple 1: Cube
3.1.1. Perspective cavalière cube
3.1.2. Axonométrique cube:
3.1.3. Cube à 1 point de fuite:
3.1.4. Cube à deux points de fuites:
3.2. Exemple 2 : Prisme à base rectangulaire
3.2.1. Cavalière prisme à base rectangulaire:
3.2.2. Axonométrique prisme à base rectangulaire:
3.2.3. Prisme à base rectangulaire: à 1 point de fuite:
3.2.4. Prisme à base rectangulaire: à deux points de fuites:
3.3. Exemple 3 : Prisme à base carrée
3.3.1. Cavalière prisme à base carrée:
3.3.2. Axonométrique prisme à base carrée:
3.3.3. Prisme à base carrée: à 1 point de fuite:
3.3.4. Prisme à base carrée: à deux points de fuites:
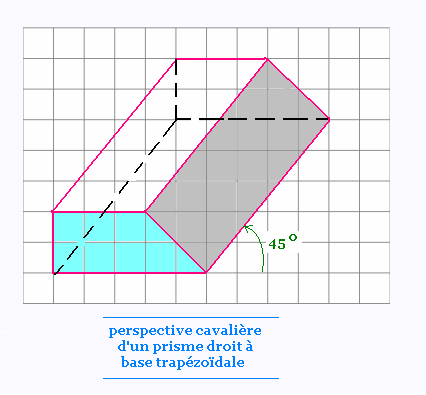
3.3.5. Cavalière prisme à base trapézoïdale:
 Â Â Â Exercises
résolus: pour FOTIOS
1. Les prismes: C'est l'exercice 10
Un prisme est polyèdre ayant deux faces
isométriques et parallèles appelées bases.
Les parallélogrammes qui relient ces deux bases sont
appelés faces latérales.
Un prisme est droit si ses faces latérales sont de
rectangles.
Un prisme est régulier s'il est droit est que la base
est un polygone régulier.
Exemple:
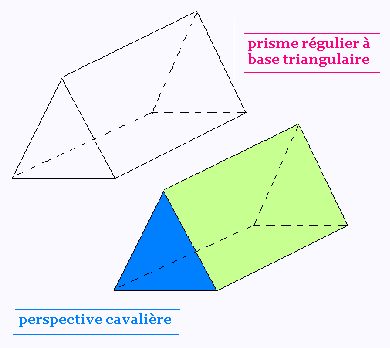
a) Prisme régulier à base triangulire:
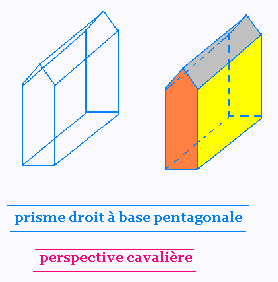
b) Prisme droit à base pentagonale:
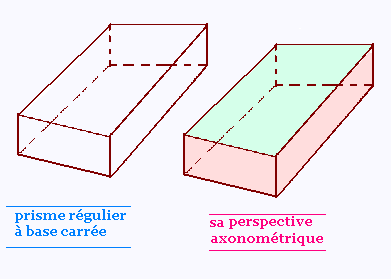
c) prisme régulier à base carrée:
2. Les tours
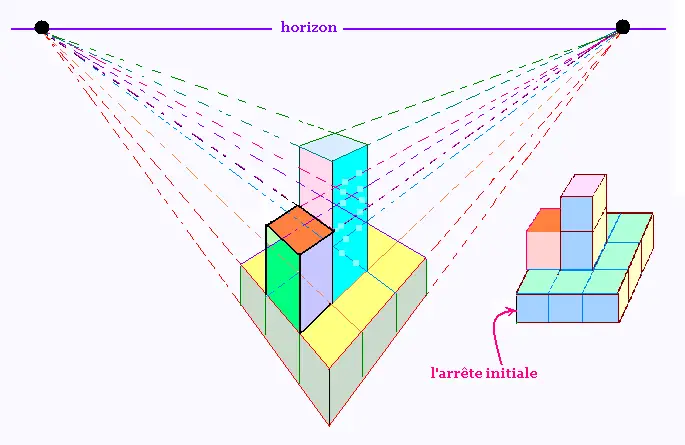
2.1. Tour 1
Toutes les quatre faces latérales sont identiques.
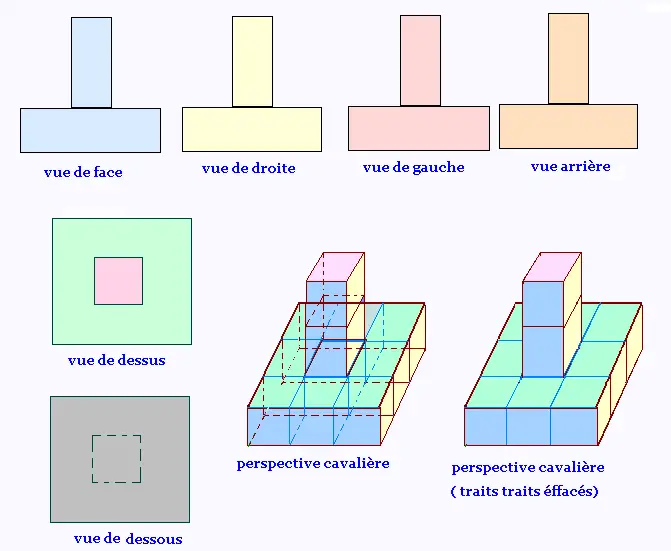
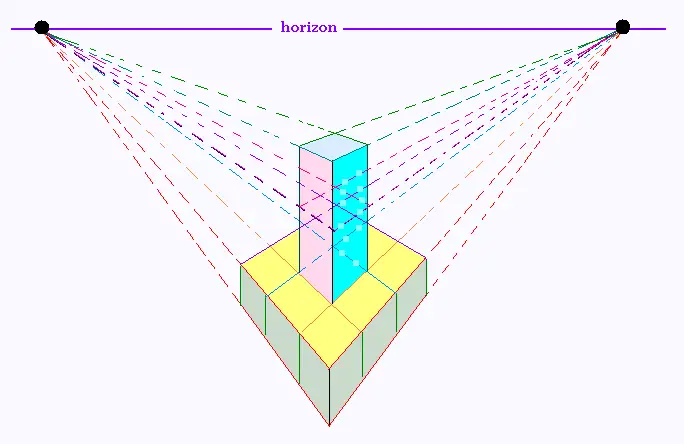
Projection centrale à deux points de fuites de cette tour.
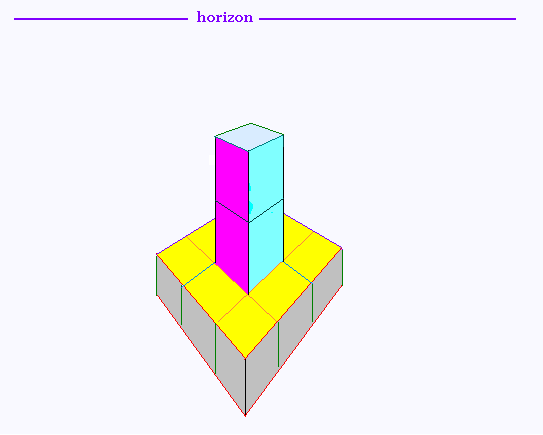
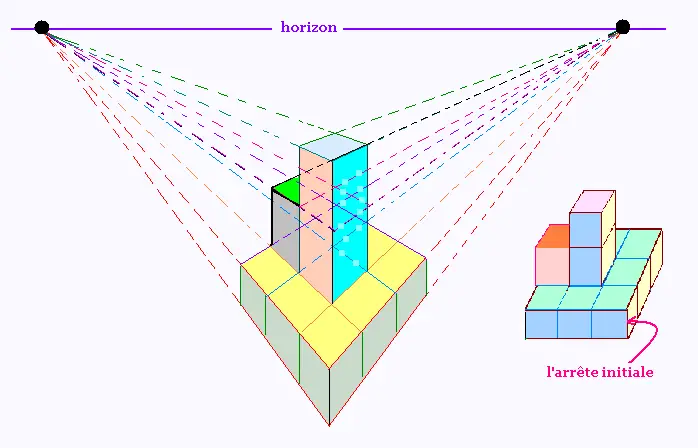
Projection centrale à deux points de fuites de cette tour,
avec suppression des fuyantes
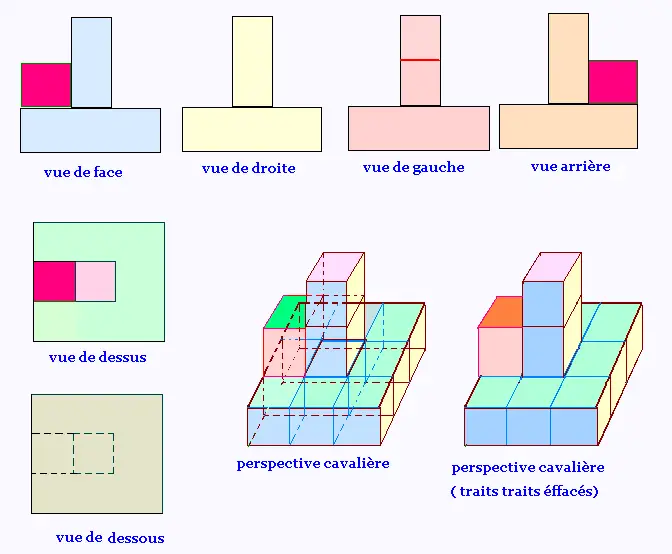
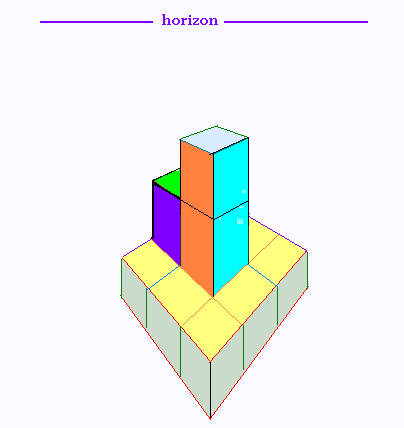
2.2. Tour 2
3. L'escalier:
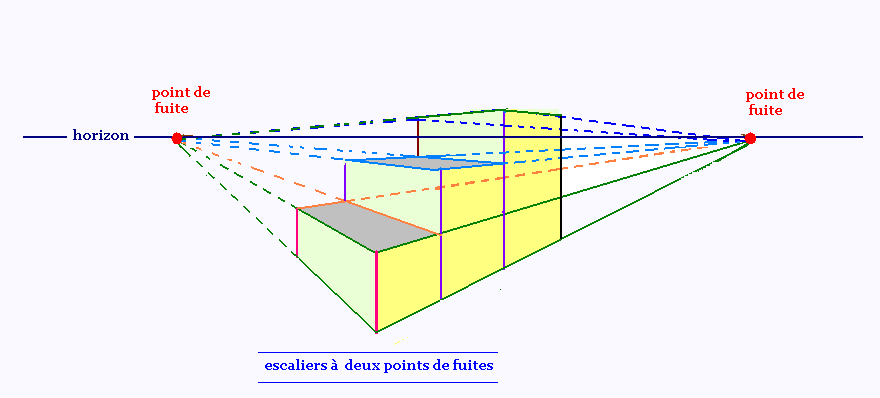
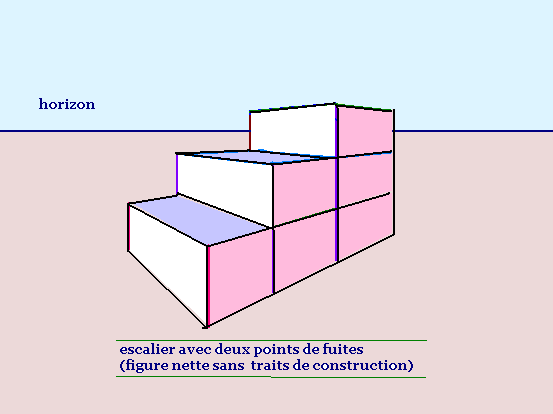
Projection centrale à deux points de fuites
d'un esclaier à 3 marches
1. Proche de l'horizon: C'est l'exercice 9
Après l'horizon, on ne voit plus les marches, mais
les contre-marches restent visibles.
En effaçant les fuyantes :
2. Loin de l'horizon
On voit les marches et les contre-marches.
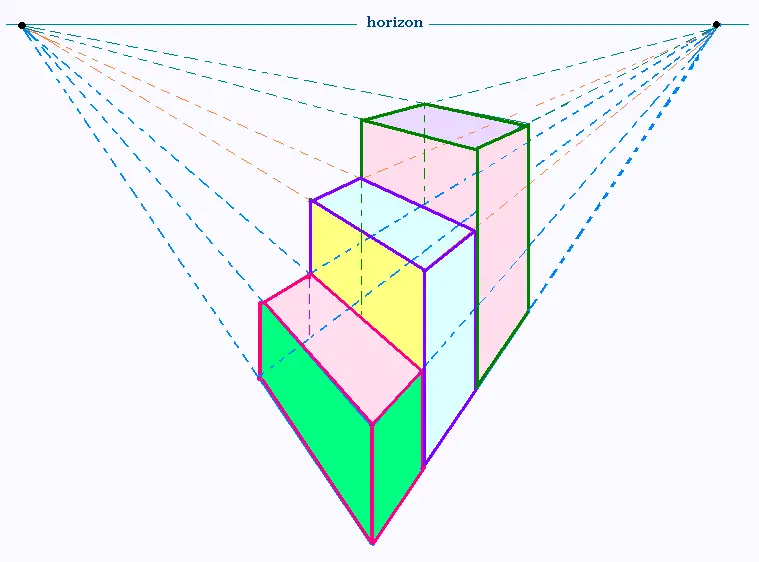
En effaçant les fuyantes :
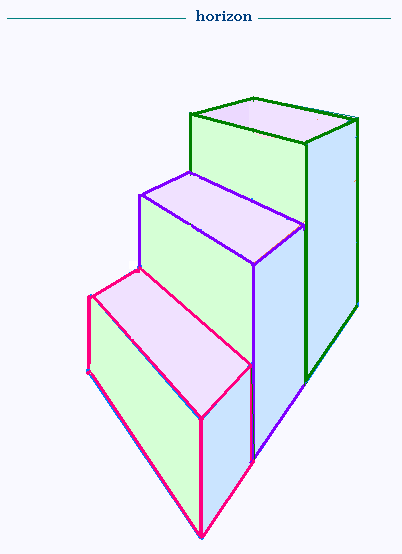
4. Rappels: Les projections et les perspectives
1. Projection:
La projection est la représentation d'un objet en 3 dimensions
sur un plan.
C'est une opération qui transforme les points et donc les
lignes d'un objet en d'autres points et lignes en traçant des droites
parallèles appelées projetantes.
Ces projections sont dites orthogonales si les
projetantes sont perpendiculaires au plan de projection.
Il esiste 3 types de projections:
Les projections sont parallèles ou centrales, ou orthogonales.
La projection parallèle contient la perspective
cavalière et la perspective axonométrique (ou isométrique).
La projection centrale contient la perspective à un point
de fuite et la perspective à deux points de fuite.
La projection orthogonale contient la vue de face ou arrière,
vue de gauche ou de droite, vue de dessus ou de dessous.
Trois vues suffisent en général pour définir un objet.
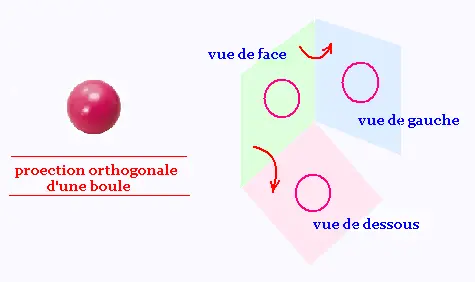
2. Perspectives
Dans la perspecticve cavalière, on commence par dessiner
une FACE frontale et on respecte le parallélisme.
L'angle de fuite est 45°.
Dans la perspective axonométrique (isométrique), on commence
par dessiner une ARÊTE et on respecte le parallélisme .
L'angle de fuite est 30°.
Dans la perspecticve centrale (ou conique) à
un point de fuite, on commence par dessiner une FACE frontale
et on respecte l'éloignement (ou ligne d'horizon).
Dans la perspective à deux points de fuite, on commence par
dessiner une ARÊTE et on respecte l'éloignement.
On retient:
• Parallèle: cavalière - face - 45o.
• Parallèle: axonométrique - arrête - 30o.
• Centrale: À 1 point de fuite - face.
• Centrale: À 2 points de fuite - arrête.
• Orthogonale : 3 faces.
5. Construction d'un solide
à partir de ses projections orthogonales
C'est l'exercice numéro 4.
Solide 1:
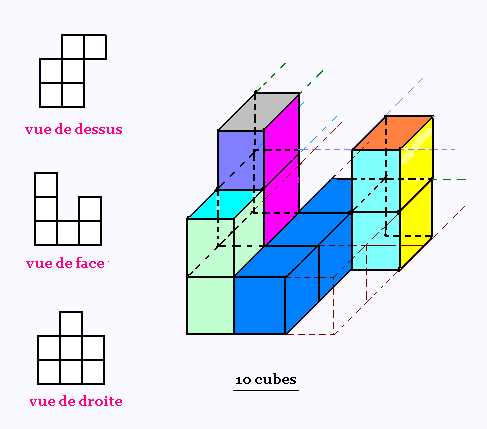
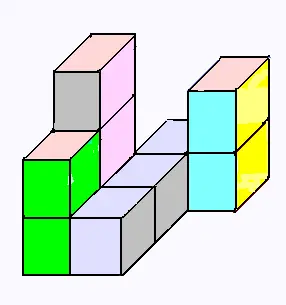
Solide 2:
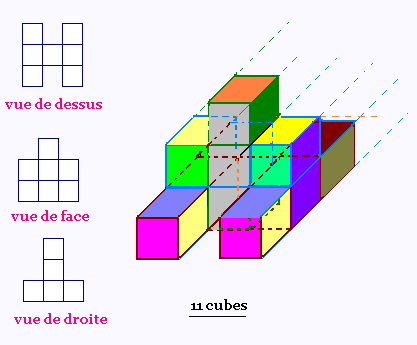
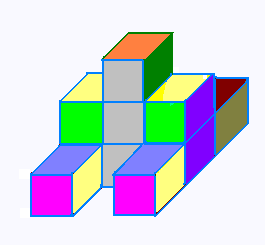
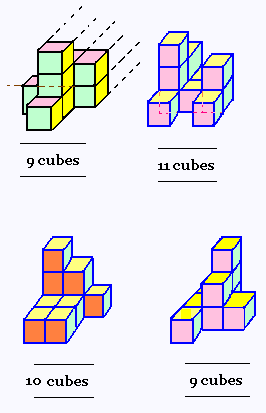
6. Vue dans l'espace:
empilements des cubes identiques
avec perspective cavalière
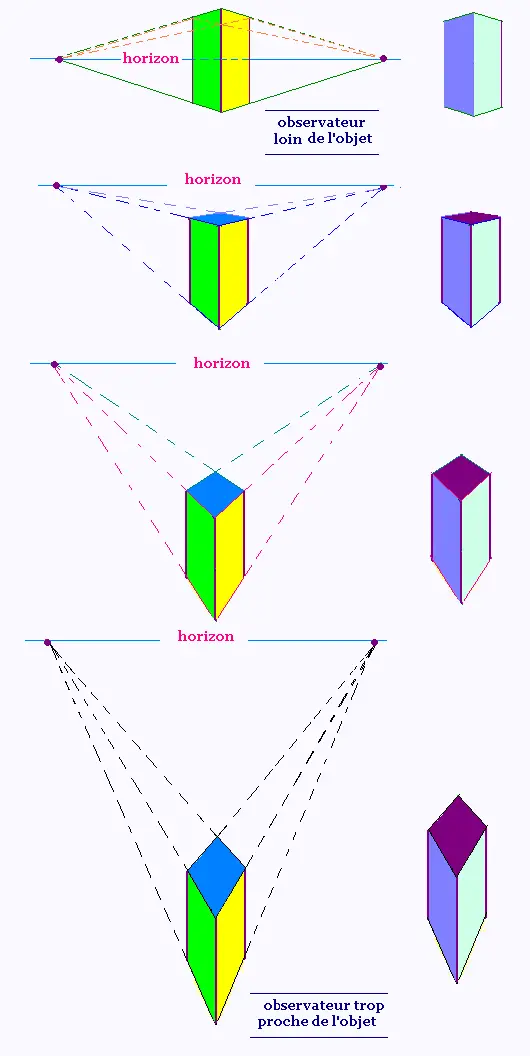
7. Vue d'un cube en :
perspective à deux points de fuite
selon la position de l'observateur
|
