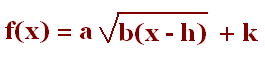Mathématiques 45: Algèbre
Racine carrée
1. Lois des exposants et des radicaux
1) n0 = 1, pour n différent de 0
2) na · nb = n(a+b)
3) na/nb = n(a-b)
4) 1/na = n(-a)
5) (n·m)a = na·ma
6) (na)b= n(a·b)
7) √n = n1/2
8) √nm = √n·√m
9) (√n)2 = n
2. Racine carré: foncions de base
La fonction carré transforme x en son carré:
y = f(x) = x2
f : x → y = f(x) = x2
Par exemple f(+2) = (+2)2 = 4 . Mais nous avons aussi
f(-2) = (-2)2 = 4
La réciproque de la fonction carré est racine carrée:
x ← y = x2
Mais pour une valeur de y, comme 4, nous avons deux valeurs
de x comme + 2 et - 2.
Donc cette réciproque n'est pas une fonction.
Pour que cette réciproque soit une fonction, on omet
l'ensemble des valeurs négatives. Ainsi la réciproque
devient bien une fonction. Le codomaine de cette fonction
réciproque n'est pas R, mais juste R+:
La racine carrée (√) est une fonction dont
le domaine est R+ et le codomaine est R+.
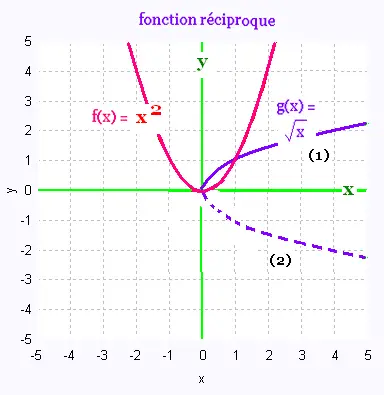
On supprime la partie (2) pour que la réciproque devienne
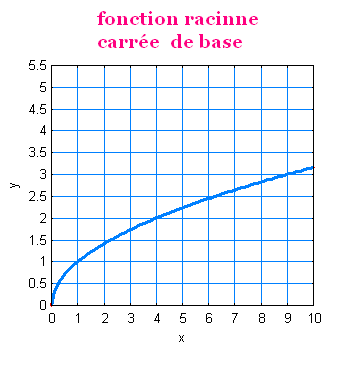
une fonction. Ainsi on obtient la fonction racine carrée
de base f(x) = √x.
3. Forme canonique
La forme canonique d'une racine carrée est:
f(x) = a√[b(x-h)]+k
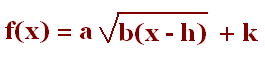
Exemples:
f(x) = 2√[3(x - 1)] + 7
f(x) = 8 √[- (x - 2)] + 1
f(x) = - 3√[5(x - 2)] - 4
f(x) = - 3√[5(x - 2)] + 6
f(x) = - 5√[- 4(x - 9)]
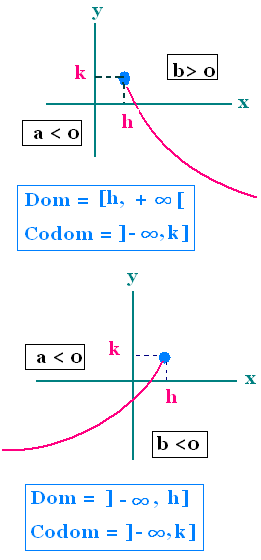
4. Propriétés des paramètres a, b, h et k
5. Example
f(x) = - 4√[1(x + 2)] - 6
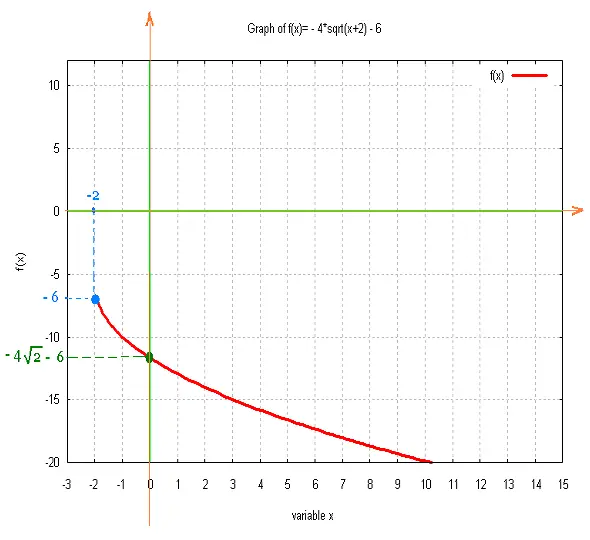
6. Zéro des fonctions racine carrée
Si le paramètre k = 0, alors , le zéro de la fonction
est égal à la valeur du paramètre h.
Pour la fonction f(x) = - 5√[- 4(x - 9)],
le zéro est x = + 9.
Si les paramètres a et k sont de mêmes signes, la
fonction n'a pas de zéro.
f(x) = 8 √[- (x - 2)] + 1 n'a pas de zéro.
Si les paramètres a et k sont de signes contraires, la fonction
admet un zéro, c'est (k/a)2/b - h .
f(x) = - 3√[4(x - 2)] + 6 admet un zéro, c'est 3.
7. Équations avec racine carrée
Pour résoudre une équation contenant une racine
carrée, on isole d'abord l'expression racine carrée et
ensuite en procède à la résolution.
Exemple:
- 3√[5(x - 2)] + 6 = 3
- 3√[5(x - 2)] = - 3
√[5(x - 2)] = 1
5(x - 2) = 1
x - 2 = 1/5
x = 2 + 1/5
x = 11/5
8. Exercices
Représenter graphiquement les fonctions suivantes
et trouver leur zéros s'ils éxistent:
f(x) = 2√[3(x - 1)] + 7
f(x) = 8 √[- (x - 2)] + 1
f(x) = - 3√[5(x - 2)] - 4
f(x) = - 3√[5(x - 2)] + 6
f(x) = - 5√[- 4(x - 9)]
|