Mathématiques 45: Algèbre
La racine carrée
1. Introduction
La racine carrée d'un nombre a est le nombre
b dont le carré b2 est égal au nombre a.
Le symbole de la racine carrée s'appelle un
radical et se note . .
Nous avons:
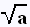 = b → a = b2 = b → a = b2
Dans l'ensemble des nombres réels, la racine carrée
d'un nombre négatif n'existe pas.
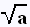 est définie si a > 0 est définie si a > 0
Le nombre a dont on extrait la racine carrée,
c'est à dire le nombre qui est sous le radical est appelé
le radicande.
2. Définition de la racine carrée
Quelles sont les solutions de l'équation x2 = a ?
Les solutions de cette équation sont
les deux nombres réels +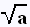 et
- et
-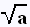 . .
Par exemple l'équation: x2 = 16
admet 2 solutions:
x = + 4 et x = - 4, puisque (+ 4)2 = 16 et (- 4)2 = 16.
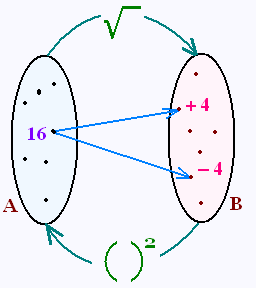
Nous avons: √16 = + 4 et √16 = - 4 .
Pour extraire la racine carrée, à un nombre de l'ensemble A correspond deux nombres dans l'ensemble B.
Réciproquement, pour élever au carré, à un nombre de l'ensemble B lui correspond un seul nombre dans l'ensemble A.
Pour avoir une bijection, c'est à dire une seule
flèche entre A et B, on élimine les nombres négatifs
de l'ensemble B.
Ainsi, on définit LA racine carrée de la façon suivante:
La racine carré d'un nombre a est le nombre POSITIF ou
NUL
b dont le carré est égal à a .
3. Propriétés de la racine carrée
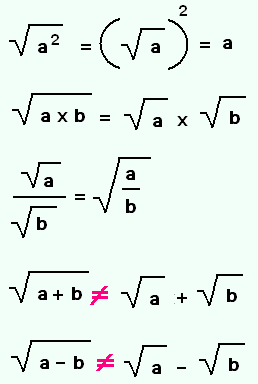
Les propriétés de la racine carrée découlent
des lois sur les puissances.
Il est très utile de se rappeler de le formule
le l'équivalence entre la racine nième et la puissance nième
d'un nombre (ici n = 2):
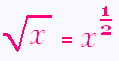
On ne peut pas défaire les opérations d'addition
ou de soustraction sous un radical.
4. Exercices
4.1. Exercice 1
Remplacer les pointillés par l'expression qui
convient:
100 est ....... de 10 ou de - 10.
100 a pour ..........10 000.
- √10 a pour ....... 10.
10 est ........ de √10 ou de -√10.
100 a pour ............10.
10 est ............. 100.
4.2. Exercice 2
Compléter:
36 est le carré de ..... ou de ......
36 a pour racine carré .........
- √5 et +√5 ont pour carré ......
16 est le carré de ...... ou de ........
- √7 et + √7 sont ....... de l'équation
x2 = ......
4.3. Exercice 3
Exprimer les nombres suivants sans les radicaux:
√36 =
√ 49 =
√144 =
(7√3)2 =
√(52) =
√0 =
(√9)2 =
(- √8)2 =
(- √4)3 =
(√(- 3)2)2 =
4.4. Exercice 4
Développer et simplifier:
5(3√2 - 2√2) =
(5√3 + √3 + 1)(√3 - 2) =
(√3 - √5)2 =
(√7 + √3)(√7 - √3) =
(4√3 - 2√5)2 =
4.5. Exercice 5
Un carrée parfait est un nombre réel
psitif qui a pour racine carrée un nombre
entier.
a)Ecrire les onzes carrés parfaits inférieurs ou
égaux à 100.
b)Donner leurs racines carrées.
4.6. Exercice 6
Calculer :
√100 - √9 + √81 =
√(16 + 9) =
√27 x √3 =
√5 x √(1/5) =
√5 x √20 =
√7 x 2√7 x 2√3 x 3√3 =
√(2/15) x √3 x √5 =
√81 x √3 x √2 x √6 =
√8 x √16 x √10 x √5 =
4.7. Exercice 7
Quelle est la condition sur x pour avoir
les expressions suivantes:
a)√(x - 1)
b)√(2x - 6)
c)√(x - 3)2
4.8. Exercice 8
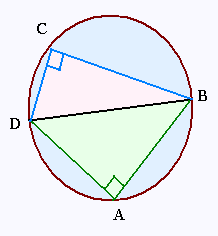
L'aire du cercle est égale à 314.16 cm2.
Les cathètes [AD] et [DC] mesurent respectivement
6 cm et 3 cm.
a) Calculer le diamètre [BD] du cercle.
b) Utiliser la formule de Pythagore pour calculer les mesures des cathètes [AB] et [BC].
c) Calculer l'aire des deux rectangles ABD et
BCD.
d) En déduire l'aire de la partie (blue) complémentaire au quadrilatère ABCD par rapport au cercle.
• ☛ Pour plus sur la racine carré
|