Mathématiques 2: Fonctions
Règle d'une fonction élémentaire

1. Comment détérminer la règle
d'une fonction élémentaire

Deux façons:

1.1. À partir du tableau de valeurs

Les résultats sont tabulés, c'est à dire les valeurs des variables x et y sont inscrits dans une table de valeur.

Si les valeurs de x sont croissantes et que les valeurs de y sont décroissantes, faire le produit de valeurs (x . y ). S’il est constant. la fonction est rationnelle. La relation entre x et y est une situation de proportionnalité inverse:
y = a/x

Dans le cas contraire, à part d'autres fonctions, nous aurons soit une fonction constante , soit une fonction linéaire, soit une fonction affine:
y = a: variation nulle,
y = ax: variation directe,
y = ax + b: variation partielle.

Dans le cas d'une variation directe y = a x, la relation entre x et y est une situation de proportionnalité . Le coefficient a est appelé coefficient de proportionnalité.

Le cas de la fonction constante est évident.

Pour les deux autres cas de fonction linéaire et affine, il suffit de poser un modèle de règle y = ax ou y = ax + b, et déterminer a et b.

1.2. À partir du graphique

Si la courbe est une droite parallèle à l'axe des x, alors la fonction est constante, de variation nulle.

Si la courbe est une droite qui passe par l'origine, alors la fonction est linéaire, de variation directe.

Si la courbe est une droite qui ne passe pas par l'origine, alors la fonction est affine, de variation partielle.

Si la courbe est une hyperbole ne traversant pas les axes, alors la fonction est rationnelle.

2. Exemples

2.1. Exemple 1

x	- 5	- 2	0	4	3	5	8
y	- 13	- 7	- 3	5	3	7	15

1. Les produits (x.y) ne sont pas constant. Ainsi la fonction n'est pas rationnelle. Elle n'est pas de la forme y = a/x. La relation n'est pas une situation de proportionnalité inverse.

2. y n'est pas constant. Ainsi la fonction n'est pas constante.

3. Les quotients y/x ne sont pas constants. Ainsi la fonction n'est pas linéaire.

4. Elle doit être affine: On pose y = a x + b . On prend deux couples de valeurs quelconques, soit (0, -3) et (4,5).

On les place dans l'équation y = a x + b, on obtient:

- 3 = a 0 + b , donc b = - 3.

5 = 4 a + b = 4 a - 3, donc 5 = 4 a - 3, d'où a = 2

L'équation s'ecrit donc y = 2 x - 3.

2.2. Exemples 2

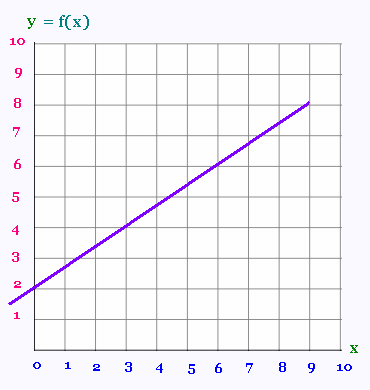
La fonction correspondante est affine puisque sa courbe est une droite qui ne passe pas par l'origine. Sa règle est y = a x + b.

La courbe est une droite qui passe par le point (0,b) = (0,2)

On ecrit y = a x + 2

On prend un autre point, par exemple le point (3,4).

4 = 3 a + 2 , donc a = 2/3

Ainsi l'équation s'ecrit:

y = (2/3) x + 2