Mathématiques 45: Géométrie:
Relations métriques dans
un triangle rectangle
1. Relations métriques
avec les rapports trigonométriques :
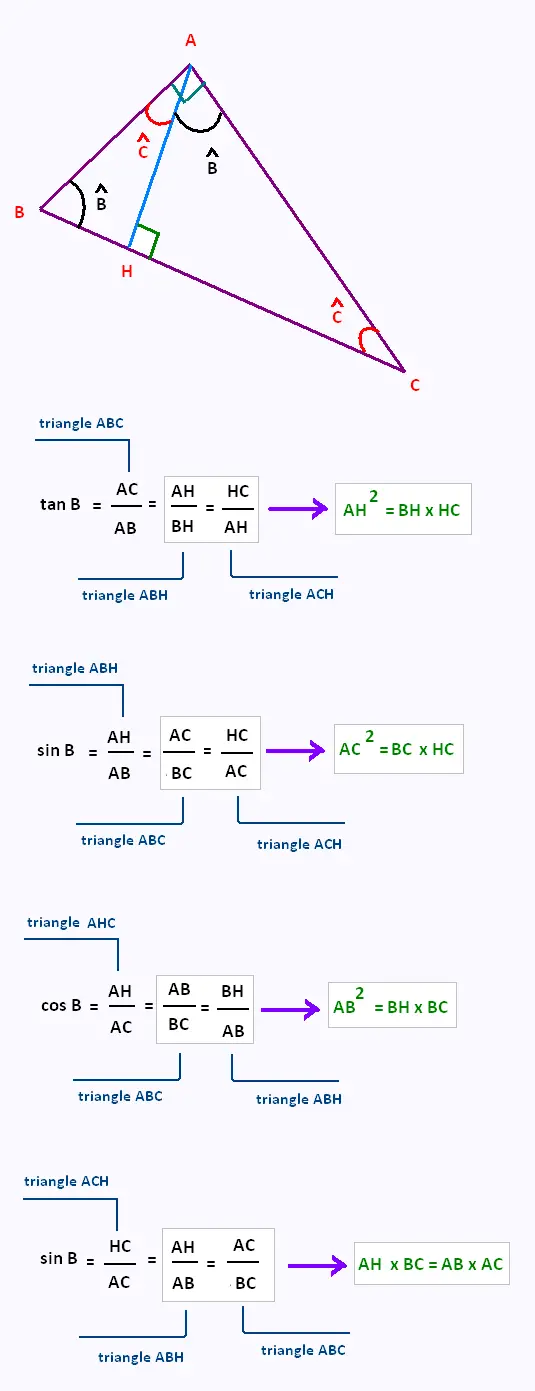
Nous allons trouver quatre relations métriques
dans un triangle rectangle, just en écrivant les
rapports trigonométriques des angles complémentaires.
1. Relations métriques par les rapports de similitude:
Nous allons trouver quatre relations métriques
dans un triangle rectangle, just en écrivant les
rapports de similitude de deux triangles semblables.
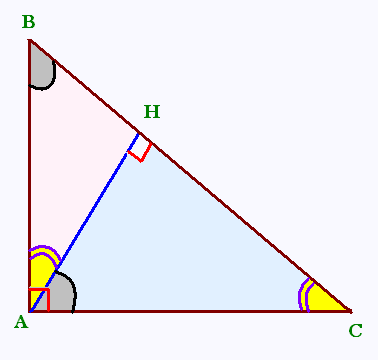
Dans le triangle ABC rectangle rectangle en A, on utlise :
. Le petit triangle rectangle ABH et le grand triangle rectangle ABC, et
. Le petit triangle rectangle ABH et le moyen triangle rectangle ACH,
. Le moyen triangle rectangle ACH et le grand triangle rectangle ABC,
pour démontrer les trois premières relations;
puis l'aire du triangle ABC pour trouver la dernière relation.
Relation 1 :
Les angles ∠HAB et ∠C sont congrues, ainsi les
triangles HAB et ABC sont semblables (cas AA).
Les rapports de similitude sont:
AB/BC = BH/AB
D'où AB2 = BC . BH
AB2 = BC . BH
Relation 2 :
Les triangles ACH et ABH sont semblables (cas AA).
Les rapports de similitude sont:
AB/AC = AH/HC = BH/AH
D'où AH2 = BH . CH
AH2 = BH . CH
Relation 3 :
Les angles ∠CAH et ∠B sont congrues, ainsi les
triangles ACH et ABC sont semblables (cas AA).
Les rapports de similitude sont:
AC/BC = CH/AC
D'où AC2 = BC . CH
AC2 = BC . CH
Relation 4 :
L'aire du triangle rectangle ABC =
AB x AC/2 = AH x BC/2.
D'où AB x AC = AH x BC
AB x AC = AH x BC
3. Exemple:
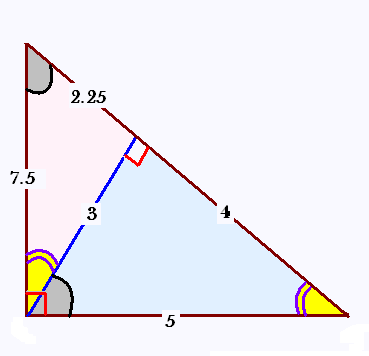
On peut vérifier que les mesures (en unités) dans ce triangle
vérifient les quatres relations métriques.
4. Exercice 1
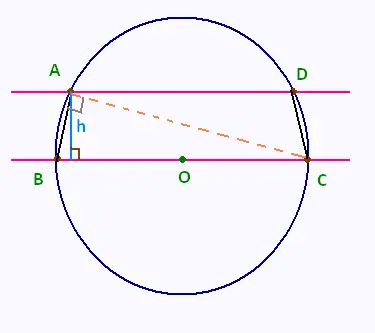
Énoncé:
Deux droies parallèles (AD) et (BC) coupent un cercle de
6.5 cm de rayon interceptent deux cordes (AB) et (CD)
mesurant 5 cm chacune.
La droite (BC) passe par le centre O du cercle.
Quelle est la distance entre ces deux droites.
Réponse:
•
On sait que le diamètre BC du cercle est égal à 2 x 6.5 = 13 cm.
De plus, le segment [BC] est un diamètre du cercle.
•
Par définition, la distance entre deux droites parallèles est la
longueur du segment entre ces deux droites qui leur est perpendiculaire. C'est à dire la valeur de h.
Le triangle ABC inscrit au cercle est rectangle en A, d'après la propriété « Si un triangle est inscrit dans un cercle de diamètre l'un de ses côtés, alors ce triangle est rectangle. »
a) Calcul de AC:
D'après la propriété de Pythagore:
AB2 + AC2 = BC2. Soit:
52 + AC2 = (2 x 6.5)2.
D'où:
AC2 = 132 - 52 = 144 . Donc
AC = 12 cm
AC = 12 cm
b) Calcul de h:
Une relation métrique dans le triangle ABC s'ecrit:
h x BC = AB x AC . D'où:
h = AB x AC /BC. Soit:
h = 5 x 12 / 13 = 4.615
h = 4.615 cm
•
La distance entre les droites parallèles (AD) et (BC)
mesure 4.6 cm.
|