Maths
- 2 -
© The scientific sentence. 2010
| |
| Mathématiques 2: Relations entre les triangles
Deux triangles sont differents, ou bien isometriques,
ou bien semblables.
La somme des angles d'un triangle est égale à 180°.
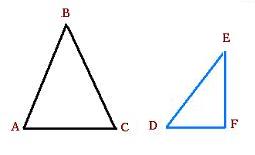
1. Triangles différents
Deux triangles sont differents si leurs angles sont différents et
leurs cotés son différents.
2. Triangles isométriques (congruence)
Deux triangles sont isométriques (congrus) si l'un est une réplique
de l'autre. L'un est l'image de l'autre par une transformation
telle que la translation, la rotation ou la reflection.
On peut les reconnaitre s'ils ont:
- Trois côtés respectivement égaux:
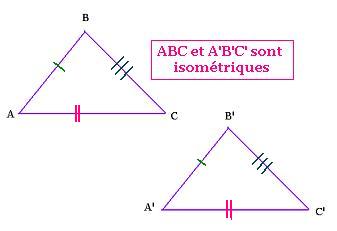
- Un angle égal, compris entre 2 cotés homologues (respectivement) égaux:
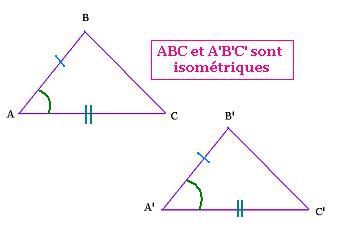
- Un côté égal compris entre 2 angles (homologues) respectivement égaux:
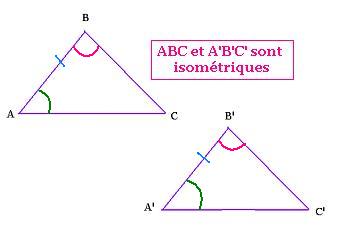
3. Triangles semblables (similitude)
Deux triangles sont semblables si l'un est un agrandissement
de l'autre.
On peut les reconnaitre s'ils ont:
- Trois côtés homologues proportionnels
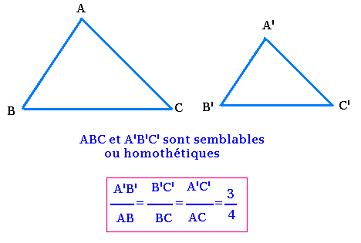
k = 3/4 est appelé rapport de similitude.
- Un angle egal compris entre deux côtés homologues
proportionnels:
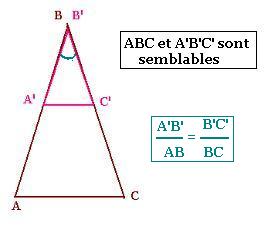
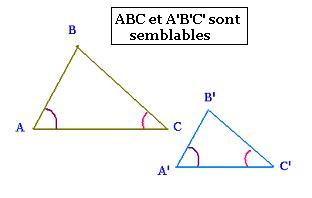
- Deux angles repectivement
égaux.
4. Propriété des triangles semblables
Deux triangles ont leurs côtés
homologues proportionnels si et seulement si leurs angles homologues sont isométriques.
Pour démontrer cette relation d'équivalence, il faut la démontrer dans
les deux sens.
1.
Si deux triangles ont leurs côtés
homologues proportionnels, alors leus
angles homologues sont isométriques.
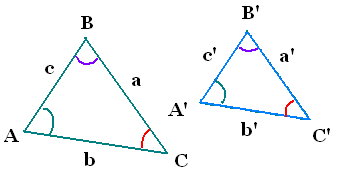
La loi des cosinus permet de le démontrer:
a2 = b2+ c2 - 2bc cos A (1)
Puisque les côtés sont proportionnels:
a'/a = b'/b = c'/c = k , alors
a'2 = b'2+ c'2 - 2b'c' cos A' =
(ka)2 = (kb)2+ (kc)2 - 2 kb kc cos A'
On simplifie par k2
a2 = b2+ c2 - 2bc cos A' (2)
Les relations (1) et (2) permettent de conclure
que mes A = mes A'
La même démonstration mène au résultas:
mes B = mes B' et mes C = mes C'
Ainsi deux triangles sont semblables si leurs côtés sont
proportionnels ou s'ils ont deux angles égaux.
2. Maintenant, on veut démontrer l'inverse:
Si deux triangles ont leurs angles homologues
isométriques, alors leurs côtés
homologues sont proportionnels.
On utilise la loi des sinus:
Pour le triangle ABC:
(sin A)/a = (sin B)/b = (sin C)/c (3)
Pour le triangle A'B'C':
(sin A')/a' = (sin B')/b' = (sin C')/c' (4)
Comme les angles homologues sont
isométriques, c'est à dire:
a = a', b = b', c = c', leurs sinus
sont aussi égaux. Ainsi, la relation (4) devient:
(sin A)/a' = (sin B)/b' = (sin C)/c' (4')
Divisant membre à membre les deus relations
(3) et (4'), il vient:
a'/a = b'/b = c'/c
C'est dire que les côtés homologues sont
proportionnels.
|
|