Mathématiques 2: Algèbre:
   Exercices de révision:
      Calcul littéral

1. Définitions:

Utiliser les expressions suivantes:

produit de facteurs,
termes identiques, et
somme de termes

pour compléter les définitions suivantes:

DEVELOPPER: C’est donner le résultat sous la forme d’une ...... ... ...... .

FACTORISER : C’est donner le résultat sous la forme d’un ....... ... ....... .

REDUIRE : C’est regrouper tous les ....... ........ .


2. Compléter:

     Développement
    --------------->
a(x + y)           ax + ...y
a(x - y)           a... - ay
(x + y)(z + t)     xz + ...t + y... + yt

    <-------------
    Factorisation


3. En utilisant la convention a x b = ab , réecrire les expressions suivantes:

A = 5 x a – 2 x b – 3 x 3 + 5 + 4a + 5y
B = 4 x a x b + 2 x cd + 5 x c – 12 x d – 4 x d x c
C = 2 x a – 5 – 5 x a² + 1 x b + 3 x c + 1 x d + 1


4. Expressions littérales

Donner la forme développée et réduite de

A = (x + 3)(2x + 1) + 4
B = 8x + 3x² + 1
C = (x + 3)² + 5

Donner la forme développée non réduite de

A = (x + 3)(2x + 1) + 4
B = 8x + 3x² + 1
C = (x + 3)² + 5
D = (x + 3)(x -4) + 3
E = (a + 3)(b -4)

Donner les expressions suivantes sous forme de produit de facteurs

A = 2x + 6
B = 8x + 4 - 3x+ 1
C = 3 - x² + 2x² - 3 + x
D = 3xy + y
E = 8xy² + xy
F = 8xy² + xy + y

Donner les expressions suivantes sous forme d'une expression littérale non développée

A = 3x² - 4x + 3
B = 8 x + 12 x² - 7
C = 4x + 16 + 1
D = - 8x + 8 -7
E = 4x² - 2x + 8


5. Réduire au maximum les expressions littérales suivantes :

A = 8x + 9 + 3x – 1 – 7x
B = - 6 – 4x + 7y – 2y + 4x
C = 4z+ 4x –3y + 3 - 4x + 6y – z
D = 6x² + 4y + 4z – 16 – 4x – 4y – 4z
E = 17z – 4 + 5x² + 1z - 15z +y – 5y
F = - (4x – 3x² + 6y) + (y² + 3x)
G = (3x – 3y + 1) – (4x + 4z) – (3x – 4y + 5z)
H = - (4x – 7x² + 3y – 4y²) + 2 – 3x² + (2x² - 3)
I = – 3(x – x² - y²)


6. Compléter les expressions littérales :

x + 4 + 4x² - 5 .... = 6x – 3x²
2(2 + ....) – 2(x + ....) = 5 + 3x² + 2x – y²
2x + 3x² - 3( ... + 4y) = x - 12y + 2x²


7. Développer et réduire les expressions littérales suivantes :

A = 2x + (3x – 3) – 5(2 + 3x)
B = - 3(x – 2) – (-x + 1)
C = 3(x² + 3) – 2(2x + x² )
D = (2x – 4)(2x - 3) – 4(x + 6)
E = (x - 2)(3 – 3x) – (-3 + 4x) – x² + x(4 – 5x)
F = 6x(4 – 2) + x² + 2(4x – 3(x² - x – 4))
G = (x + 5)²
H = (x - 1)(x + 5)²


8. Calculer la valeur des expressions littérales suivantes pour x = -1

A = 8(xsup>2 + 6) – x
B = 6x² + 3x + 3
C = 4(4x² -x + 4)


9. Développer et réduire les expressions
littérales ci-dessous :

A = 2 [4x(2 – x) + x] – x(6 – x) + x² - 5
B = (x – 6)[4 + 2x + 3(x – 1) + 2]
C = 2/4 x [(3/4) x + 1] – (1/4)x
D = [(1/2) x – 3/5](x + 4/3)


10. Factoriser les expressions suivantes :

A = 3x - 3
B = 4x² + 2x
C = (2 – x)(2 + 3x) – (2 – x)
D = (7x – 8)(1 + 3x) – (1 + 3x)²


11. Calculer la valeur des expressions suivantes pour x = 0 et y = - 1

A = 2(x² + y) – 3(x² - x + y)
B = - (2x² + 3x + 5y) – (y² + 2x)
C = 4y² - 2x - 2xy + 14


12. Factoriser, développer et réduire :

A = 2(x + 1)(3x – 3) + (x + 1)

a) Factoriser A
b) Développer puis réduire A
c) Vérifier que pour x = 1, A = 2 en utilisant :
l’expression littérale d’origine
l’expression littérale factorisée
l’expression littérale développée


13. Expressions littérales et géométrie:



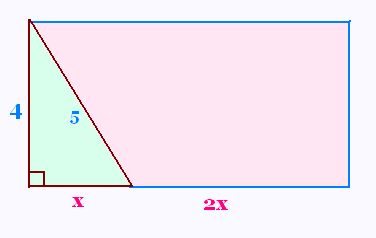
a) Calculer le périmètre P1 du triangle en fonction de x, donner le résultat sous la forme d’une expression littérale.

b) Calculer le périmètre P2 du trapèze en fonction de x, donner le résultat sous la forme d’une expression littérale.

c) Calculer le périmètre du triangle, le périmètre du trapèze et le périmètre du rectangle pour x = 1.

d) Quelle est la valeur correcte de x?

e) Utiliser l'inégalité triangulaire pour trouver toutes les valeurs entières de x.


N. B. on peut utiliser la droite numérique suivante: