Mathématiques 2: Fonctions
Taux de variation

1. Définitions

Le taux de variation détermine comment varie la variable dépendante y par rapport à la variation de de la variable indépendante x .

Exemple:

Le temps passe: variable indépendante.
La population mondiale augmente: variable dépendante Elle augmente au fur et à mesure que le temps passe.

Le taux de variation de la population est mesuré par le rapport ou plus précisément le taux:

τ = (variation de la population)/(variation du temps)

La population mondiale est estimée à 7 milliards en 2011, alors qu'elle était seulement de 6.1 milliards en 2000.

Son taux de variation est donc:

τ = (7 - 6.1)/(2011 - 2000) = 0.9/11 = 0.082.
Soit un accroissement de 82 millions d'habitons par an.

2. Taux de variation

2.1. Définition

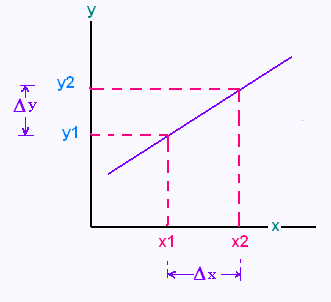
Le taux de variation détermine la valeur de l’inclinaison d’une droite.

Si y1 est la valeur de la variable dépendante correspondante à la valeur x1 de la variable indépendante, et
y2 la valeur de la variable dépendante correspondante à la valeur x2 de la variable indépendante, on note Δy = y2 - y1 la variation de y et Δx = x2 - x1 celle de x.

On ecrit ainsi le taux de variation τ sous l'expression:

τ = Δy/Δx = (y2 - y1)/(x2 - x1)

Le taux de variation est égale à la variation des y sur la variation des x.

C'est aussi le taux de variation de la fonction ƒ telle que y = ƒ(x).

2.2. Signe du taux de variation

Si la droite (ou la courbe de la fonction) est croissante (monte), le taux de variation est positif.

Si la droite (ou la courbe de la fonction) est décroissante (descend), le taux de variation est négatif.

3. Exemples

3.1. Exemple 1

Un bébé a pesé 3.2 kg à sa naissance. Pendant les trois premiers mois, il prenait du poids de 27 g par jour.

3.2 kg est le poids est la valeur initiale. 27 g est le taux de variation. Le poids est la variable y et jour est la variable x.

3.2. Exemple 2

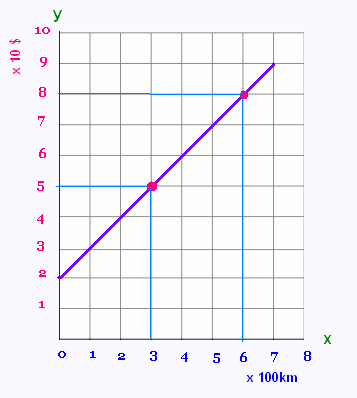
On considère le graph suivant de la fonction &nof; telle que:

ƒ(x) = 0.1 x + 20

Quel est so taux de variation ?

τ = (80 - 50) /(600 - 300) = 3/30 = 0.1.

La droite est croissante, le taux de variation est positif.

3.3. Exemple 3

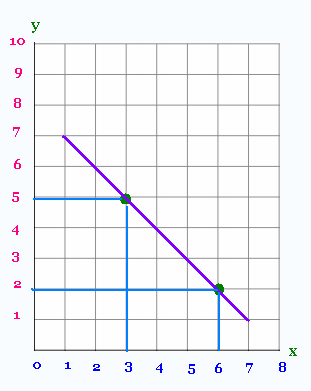
On considère le graph suivant de la fonction ƒ:

Quel est son taux de variation ?

τ = (5 - 2) /(3 - 6) = 3/ (- 3) = - 1.

La droite est décroissante, le taux de variation est négatif.

4. Taux de variation des fonctions élémentaires

4.1. Fonction constante

f(x) = a
y1 = f(x1) = a,
y2 = f(x2) = a,
τ = (y2 - y1)/(x2 - x1) = (a - a)/(x2 - x1) = 0

Fonction constante: f(x) = a, τ = 0.

4.2. Fonction linéaire

f(x) = a x
y1 = f(x1) = a x1,
y2 = f(x2) = a x2,
τ = (y2 - y1)/(x2 - x1) = (a x2 - a x1)/(x2 - x1) = a(x2 - x1)/(x2 - x1) = a

Fonction linéaire: f(x) = a x, τ = a.

4.2. Fonction affine

f(x) = a x + b
y1 = f(x1) = a x1 + b,
y2 = f(x2) = a x2 + b,
τ = (y2 - y1)/(x2 - x1) = [(a x2 + b) - (a x1 + b)]/(x2 - x1) = a(x2 - x1)/(x2 - x1) = a

Fonction affine: f(x) = a x + b, τ = a.

4.2. Fonction rationnelle

f(x) = a/x
y1 = f(x1) = a/x1 ,
y2 = f(x2) = a/x2,
τ = (y2 - y1)/(x2 - x1) = (a/x2, - a/x1)/(x2 - x1) = a(1/x2, - 1/x1)/(x2 - x1) = a(x1 - x2)/x1 x2 (x2 - x1) = - a/x1x2

Fonction rationnelle: f(x) = a/x,
τ n'est pas constant.

5. Droites et taux de variation

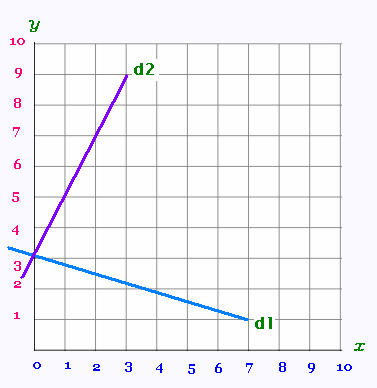
La droite d2 a pour equation: y = - (2/7) x + 3.

La droite d1 a pour equation: y = 2 x + 3.

Le taux de variation passe de - (2/7) à 2.

Lorsqu'on augmente du taux de variation, la droite subie une rotation anti-horaire autour du centre de rotation, qui est le point (0,b).

De même, une diminution du taux de variation engendre une rotation horaire dautour du centre de rotation, qui est le point (0,b).

Deux droites qui ont le même taux de variation sont parallèles.

Deux droites qui n’ont pas le même taux de variation sont dites sécantes.

Deux droites dont le produit des taux de variation est égal à - 1 sont perpendiculaires.