Maths
- 2 -
© The scientific sentence. 2010
| |
|
Math魡tiques 45: Alg袲e:
Trin𭥠Factorisation
La forme g鮩rale d'un trin𭥠du second
degr頥st:
a x2 + b x + c
a, b, et c sont des co馦icients constants.
Exemple:
2 x2 - 3 x + 7.
1. Bin𭥠du second degr鼯h3>
Un bin𭥠du second degr頥st de la forme:
a x2 + b x
C'est un trin𭥠du second degr頡vec c = 0.
Sa forme factoris饠est :
x (a x + b)
Exemple:
2 x2 - 3 x = x (2 x - 3)
2. Trin𭥠carr頰arfait
Un polyn𭥠est un trin𭥠carr頰arfait
si sa forme factoris饠 est de la forme:
a(x + b)2
Exemple:
8 x2 + 24 x + 18 = 2 (2 x + 3)2
Comment reconnaitre un trin𭥠carr頰arfait?
- On part de la forme g鮩rale a x2 + b x + c,
- On calcule le carr頤e b, soit b2,
- On calcule le produit 4 a c ,
- On fait le test suivant:
Si b2 = 4 a c, alors le trin𭥠est carr頰arfait,
On ecrit
a x2 + b x + c = a(x + b/2a)2
Si b2 ≠ 4 a c, alors le trin𭥠n'est pas un carr頰arfait.
Exemple 1:
P = 3 x2 - 12 x + 12.
b2 = (- 12)2 = 144,
4 a c = 4 (3) (12) = 144,
b2 = 4 a c, donc le trin𭥠est carr頰arfait,
Ainsi :
P = 3 x2 - 12 x + 12 = 3[x + (-12)/2(3)]2 =
3[x - 12/6]2 = 3(x - 2)2
Exemple 2:
P = x2 + 2 x + 3
b2 = (2)2 = 4,
4 a c = 4 (1) (3) = 12,
b2 ≠ 4 a c, donc le trin𭥠n'est
pas carr頰arfait.
3. Diff鲥nce de carr鼯h3>
Si on d鶥loppe la forme factoris饠d'une expression
alg颲ique (a + b)(a - b), on trouve:
(a + b)(a - b) = a2 - b2.
G鮩ralemet, avec n'importe quelles expressions
♣ et ♥,
on a toujours l'identit頳uivante:
♣2 - ♥2 = (♣ + ♥)(♣ - ♥)
Exemples:
52 - 32 = (5 + 3 )(5 - 3)
(ab)2 - 12 = (ab + 1 )(ab - 1)
(x√y)2 - (-2)2 = (x√y - 2)(x√y +2)
On remarque qu'on extrait la racine carr頍
de chaque terme.
Pour un binome su second degr鬠on a:
ax2 - b = a[x2 - b/a] =
a[x2 - (√(b/a))2] =
a[x - √(b/a)][x + √(b/a)]
ax2 - b = a[x - √(b/a)][x + √(b/a)]
Exemples:
x2 - 4 =
x2 - 22 = (x + 2 )(x - 2)
La forme factoris饠de x2 - 4 est (x + 2 )(x - 2)
3x2 - 15 =
3[x - √(15/3)][x + √(15/3)] =
3(x - √5)(x + √5)
La forme factoris饠de 3x2 - 15 est 3(x - √5)(x + √5)
3. Compl鴩on du carr鼯h3>
Dans le cas où un trin𭥠ne peut pas se
factoriser sous la forme d'un trin𭥠carr頰arfait,
ou diff鲥nce de carr鳬 on utilise la m鴨ode de
compl鴩on du carr鼯i>.
la m鴨ode de compl鴩on du carr鼯b> utilse
celle du trin𭥠carr饠parfait suivie de la diff鲥nce
de carr鮠
Partons de la forme g鮩rale: ax2 + bx + c.
1. Mettons a en facteur: a[x2 + (b/a)x + (c/a)]
On consid貥 maintenant le trin𭥺
P = x2 + (b/a)x + (c/a)
2. Cherchons le trin𭥠carr饠parfait:
Pour avoir un carr鬠on transforme les deux premiers
termes :
x2 + (b/a)x = x2 + 2(b/2a)x +
(b/2a)2 - (b/2a)2 + (c/a)
P = (x + (b/2a))2 - (b/2a)2 + (c/a)
3. Faisons apparaitre une diff鲥nce de deux carr鳺
p = (x + (b/2a))2 - [(b/2a)2 - (c/a)] =
(x + (b/2a))2 - (√([(b/2a)2 - (c/a)))2] =
(x + (b/2a) - √((b/2a)2 - (c/a)))(x + (b/2a) + √((b/2a)2 - (c/a)))
Ainsi
La forme factoris饠de ax2 + bx + c est
a (x + (b/2a) - √((b/2a)2 - (c/a)))(x + (b/2a) + √((b/2a)2 - (c/a)))
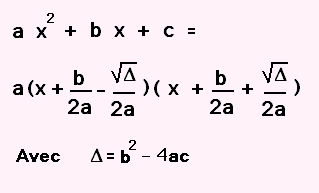
Exemple :
P = 2x2 + 2 x - 4 .
P = 2(x2 + x - 2) .
x2 + x = x2 + 2 (1/2) x + (1/2)2 - (1/2)2 =
[x + (1/2)]2 - (1/2)2
Donc:
x2 + x - 2 = [x + (1/2)]2 - (1/2)2 - 2 =
[x + (1/2)]2 - 9/4 =
[x + (1/2)]2 - [3/2]2 =
[x + (1/2) - 3/2][x + (1/2) + 3/2] =
[x - 1][x + 2]
Ainsi
P = 2[x - 1][x + 2]
La forme factoris饠de 2x2 + 2 x - 4 est
2(x - 1)(x + 2)
4. Trin𭥠sous form a(x - h)2 + k
On veut ecrire le trin𭥠de forme g鮩rale
ax2 + bx + c sous la forme suivante:
a(x - h)2 + k.
On a d骠 鴡blit la forme factoris饠suivante:
ax2 + bx + c = a (x + (b/2a) - √((b/2a)2 - (c/a)))(x + (b/2a) + √((b/2a)2 - (c/a)))
En utilsant l'identit麍
(♠ + ♦)(♠ - ♦) =
♠2 - ♦2, ou en d鶥loppant,
on obtient:
a (x + (b/2a) - √((b/2a)2 - (c/a)))(x + (b/2a) + √((b/2a)2 - (c/a))) =
a [(x + (b/2a))2 - √((b/2a)2 - (c/a))2] =
a [(x + (b/2a))2 - (√((b/2a)2 - (c/a)))2] =
a [(x + (b/2a))2 - ((b/2a)2 - (c/a))] =
a(x + (b/2a))2 - ((b2/4a) - c) =
a(x - (- b/2a))2 + ((- b2/4a) + c).
On ecrit:
h = - b/2a et k = - b2/4a + c.
Ce qui permet d'ecrire
ax2 + bx + c = a(x - h)2 + k
ax2 + bx + c = a(x - h)2 + k
avec h = - b/2a et k = - b2/4a + c.
Exemple :
3x2 + 12x + 2
h = - b/2a = - 12/(2x3) = - 2 et
k = - 122/(4x3) + 2 = - 12 + 2 = - 10.
Donc:
3x2 + 12x + 2 = 3(x + 2)2 - 10
.
|
|