Mathématiques
1ère S
Maths 1S programme
Analyse
Géométrie
Exercices
Probabilités &
Statistiques
Applications
Suites & Séries
Calculateurs
Algèbre linéaire
© The scientific sentence. 2010
|
Mathématiques 3: Probabilités
Convergence en loi
Théorème de Moivre-Laplace
1. Théorème de Moivre-Laplace
Si la variable Xn suit une loi binomiale
d'ordre n et de paramètre p appartenat à ]0,1[,
alors la variable
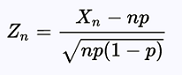
converge en loi vers une loi normale centrée et
réduite N(0,1).
Abraham de Moivre établit ce théorème en
1733, dans le cas particulier p = 1/2. Laplace le généralisa
en 1812 pour toute valeur de p comprise entre 0 et 1.
Il s'agit d'un cas particulier du théorème central limite,
qui est plus général.
2. Théorème de la limite centrale
Le théorème central limite, aussi appelé théorème de la limite
centrale ou centrée, établit la convergence en loi de la somme d'une
suite de variables aléatoires vers la loi normale.
Ce résultat affirme que toute somme de variables aléatoires
indépendantes et identiquement distribuées tend vers une
variable aléatoire gaussienne.
La première démonstration de ce théorème fut
publiée en 1809 par Pierre-Simon de Laplace.
3. Loi Normale
La loi normale est l'une des lois de probabilité les plus
adaptées pour modéliser des phénomènes naturels issus de plusieurs
événements aléatoires.
Elle est également appelée loi gaussienne, loi de Gauss ou loi de
Laplace-Gauss.
La loi normale est une loi de probabilité absolument continue
qui dépend de deux paramètres : son espérance μ, et
son écart type σ, un nombre réel positif.
La densité de probabilité de la loi normale est donnée par :
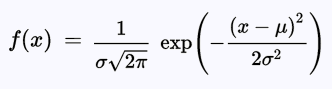
La loi normale de moyenne nulle μ = 0 et d'écart type unitaire
σ = 1 est appelée loi normale centrée réduite
ou loi normale standard.
Lorsqu'une variable aléatoire X suit la loi normale,
elle est dite gaussienne ou normale. On utilise alors
la notation suivante X ≈ N(μ, σ2).
La loi normale standard est donc noté N(0, 1).
4. Courbe encloche
Graphique de loi normale centrée non réduite
ou courbe encloche:
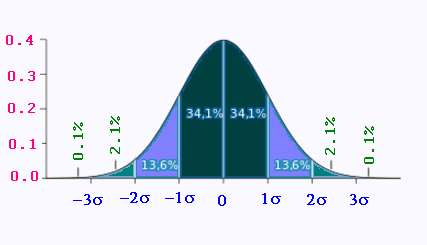
|
|