Mathématiques 3: Algèbre linéaire
Chaîne de Markov

Chaîne de Markov

1. Définition

Le modèle de Markov, est aussi appelé Chaîne de Markov. C'est un modèle statistique qui utilise les matrices et les probabilités.

Dans ce modèle, la matrice représente une transition. Cette transition matérialise la possibilité pour un système de passer d'un état à un autre.

Si l'on suppose que le système, dans un état i à l'instant t passe à l'état j à l'instant ultérieur t+1, la probabilit pij(t) de ce passage constitue l'élement de matrice correspondant de la matrice de transition P.

On supposera que la probabilité pij(t) est indépendente de t. De plus, le temps t est discret, avec un ensemble fini d'états.

Dans le modèle de Markov, les transitions sont unidirectionnelles : une transition de l'état A vers état B ne permet pas d'aller de l'état B vers l'état A.

Tous les états ont des transitions vers tous les autres états, y compris vers eux-mêmes. Chaque transition est associée à sa probabilité d'être empruntée et cette probabilité peut éventuellement être nulle.

On peut donc décrire le système en donnant l'ensemble {u1, ..., um} des états ui possibles et une matrice P de dimensions m x m dont le terme pij est la probabilité que le processus soit dans l'état j à l'instant t+1 étant donné qu'il se trouve dans l'état i à l'instant t, pour tout t. P est appelée matrice de transition du système.

On représente généralement P par un graphe orienté G dont les sommets ou noeuds) correspondent aux m états et les arcs aux couples ordonnés d'états (i,j) tels que p_ij > 0, c'est à dire aux probabilités de transition.

Un état du système est un vecteur ligne.

2. À propos de Markov

Andrei Andreievitch Markov (1856 - 1922) est un mathématicien russe. Il étudia à l'université de Saint-Pétersbourg en 1874.

Ses travaux sur la théorie des probabilités l'ont amené à mettre au point les chaînes de Markov qui l'ont rendu célèbre.

3. Exemple 1

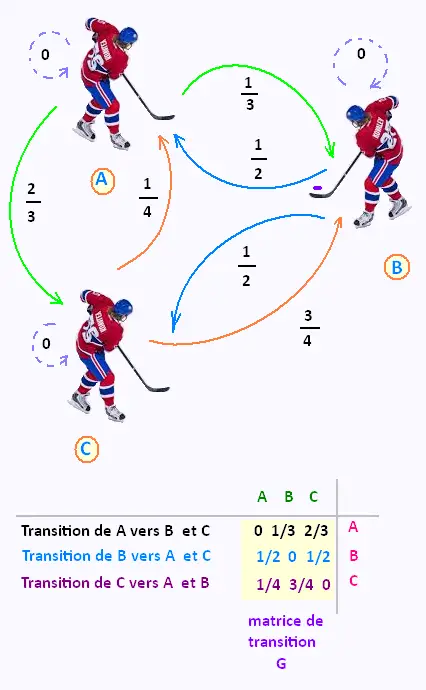
Dans une équipe de Hockey, on étudie les passes de la rondelle que font les trois joueurs A , B et C entre eux.

Les probabilités qu'un joueur passe la rondelle à un autre sont représentées sur le graph suivant ci-contre.

À partir de ce graphe G , on en déduit la matrice de transistion G correspondante.

Si c'est le joueur B qui possède la rondelle à l'étape 0, quelle est, par exemple la brobabilité que le joueur C la possède après la troisième étape?

Initialement la rondelle est en B, donc le vecteur état du système est Po = (0, 1, 0). Après 3 étapes, l'état du système est P3 = Po G³ . Il suffit de calculer le cube G³ de la matrice de transition G et puis de multiplier le vecteur Po par G³.

La brobabilité que le joueur C possède la rondelle après la troisième étape est la troisième composante du vecteur P3 trouvé.

Du fait que Po = (0, 1, 0) et que seule la troisième composante du vecteur P3 nous interesse, le terme à retenir est donc p⁽³⁾₂₃, qui est 17/48 = 0.3542

P3 = 35.42%

Nous avons environ 35% de chance que la rondelle se trouve chez le joueur C après trois passes.

3. Exemple 2 Chaîne de Markov pour
une pièce non-truquée.

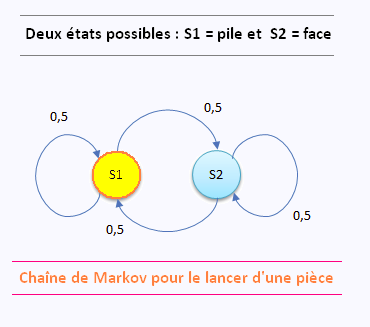Sur cette chaîne de Markov, les états sont notés par des cercles et les transitions par des flèches partant de l’état initial vers l’état final et ayant une valeur qui est la probabilité de transition. La somme des probabilités sortant d’un état est toujours égale à 1.

3. Exemple 3

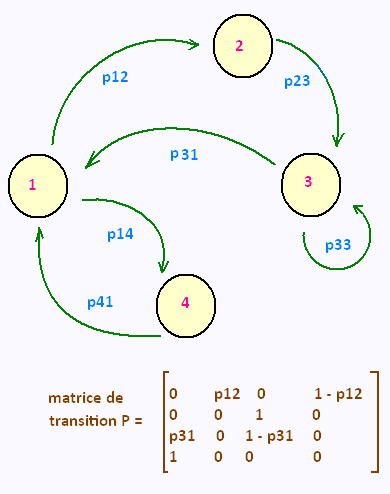
Les chaînes de Markov peuvent être représentées graphiquement sous la forme d'un graphe orienté. On associe alors un nœud à chaque état et un arc orienté à la probabilité de transition.

On veut, à partir de ce graph, établir la matrice de transition.

L'ensemble des état est E = {1, 2, 3, 4}.

On a :

p11 = p22 = p44 = 0
p23 = p41 = 1
p12 + p14 = 1
p33 + p31 = 1

4. Chaîne de Markov

4.1. Processus stochastique

Un processus stochastique est une suite d'expériences dont le résultat dépend du hasard. C'est aussi un processus aléatoire dont le résultat n'est pas connu avec certitude.

Ce qui est aléatoire, relève du hasard et donc du calcul des probabilités. Un phénomène stochastique dépend de variables aléatoires. Pour l'étudier, on procède donc à une analyse statistique.

Ici, nous admettrons qu'en certains temps 0, 1, 2, ..., t, nous observons un système. Celui-ci peut se trouver dans l'un des états d'une collection finie d'états possibles. L'observation du système est ainsi considérée comme une expérience dont le résultat (aléatoire) est l'état dans lequel se trouve le système.

Un processus stochastique {X(t)}t T est une fonction du temps dont la valeur à chaque instant dépend de l'issue d'une expérience aléatoire réalisée à l'instant t.

A chaque instant t T , X(t) est donc une variable aléatoire. Si l'on considère un temps discret on note alors {X_n}n n N un processus stochastique à temps discret.

Si l'on supposeenfin que les variables aléatoires X_n ne peuvent prendre qu'un ensemble discret de valeurs, on parlera de processus à temps discret et à espace d'état discret.

4.2. Chaîne de Markov

Une chaîne de Markov est un type particulier de processus stochastique qui vérifie deux conditions :

• L'état au temps t du processus ne dépend que de son état au temps t - 1 :

P(Xt = j|X1 = i1,... ,Xt-1 = it-1) = P(Xt = j|Xt-1 = it-1)

• La probabilité de passage d'un état i à un état j ne varie pas avec le temps :

t [1, N] P(Xt = j|Xt-1 = i) = Constante.

La probabilité pour que la chaîne soit dans un certain état à la ième n étape du processus ne dépend donc que de l'état du processus à l'étape précédente (la ième n -1 ) et pas des états dans lequel il se trouvait aux étapes antérieures.

Une chaîne de Markov est dite homogène lorsque cette probabilité ne dépend pas de n.

Généralement, la probabilité de transition d'un état i vers un état j notée p_ij :

p_ij = P(X_n = j |X_n-1) n N

En introduisant l'ensemble des états possibles noté E, on a pour j E:

Σp_ij = 1

On définit alors la matrice de transition P par :

4.3. Régime transitoire

L'analyse du régime transitoire d'une chaîne de Markov consiste à déterminer le vecteur p(j, n) des probabilités d'être dans un état j à l'étape n :

pj(n) = [pj1 (n) pj2 (n) ... pjM(n)] où M = Card(E).

Ce vecteur de probabilités dépend de la matrice de transition P, et du vecteur de probabilités initiales p(0)

Ce vecteur ligne de probabilité peut s'exprimer en fonction de la matrice de transition P :

p_j(n) = p_j(n - 1) P

En utilisant n fois cette expression, il vient :

p_j(n) = p_j(0) Pⁿ

5. Exemple 1 : chaîne de Markov à deux états

Un individu pauvre a une chance sur 3 de devenir riche.
Un individu riche a une chance sur 6 de devenir pauvre.

On représente une chaîne de Markov avec une matrice de transition.

Chaque rangée de la matrice correspond à un état et donne la probabilité de passer d'un état à un autre état.

Les états sont:

état i = pauvre
état j = riche

L'élément de matrice est:

pij: passer de i = 1 = pauvre à j = 2 = riche

p11: rester pauvre = 1 - 1/3 = 2/3
p12: passer de pauvre à riche = 1/3
p21: passer de riche à pauvre = 1/6
p22: rester riche = 1 - 1/6 = 2/3

La matrice de transition se construit donc ainsi:

	pauvre	riche
pauvre	2/3	1/3
riche	1/6	5/6

Une matrice de transition se reconnaît parce que toutes les valeurs sont entre 0 et 1 inclusivement et que la somme de chaque rangée (ligne) est égale à 1.

Pour avoir une chaîne de Markov, il faut répéter le nombre de transitions le plus possible.

Supposons qu'à chaque année qui passe, la matrice de transition s’applique.

On considère un individu qui n'est pas riche au départ, c'est à dire dans l'état [1, 0]. près une année il y aura une probabilité de 1/3 qu'il devienne riche:

La matrice de transition étant:


Alors:

[1, 0] P = [2/3, 1/3]

Après deux années, il aura autant de possibilités d’être riche que de ne pas l'être :

[1, 0] P² = [1/2, 1/2]

Et ainsi de suite.


Après un très long délai, disons 100 ans , quelle seront alors les chances?

Il suffit de calculer les puissances de la matrice de transition. On constate ici que ces puissances convergent rapidement vers une matrice fixe.

On voit, par ces matrices, qu’après 5ans, 10 ans ou 100 ans, un individu, qu’il débute comme riche ou pauvre, aura une probabilité de 2/3 = 0.66666 = 66.66% d’être riche.