Mathématiques
1ère S
Maths 1S programme
Analyse
Géométrie
Exercices
Probabilités &
Statistiques
Applications
Suites & Séries
Calculateurs
Algèbre linéaire
© The scientific sentence. 2010
|
Mathématiques 3: Akgèbre
Les suites
Suite de Syracuse
Suite de Syracuse
Au début des années 1930, un mathématicien de l'université de Hambourg ,
Lothar Collatz, proposa de faire des suites de nombres de la
manière suivante :
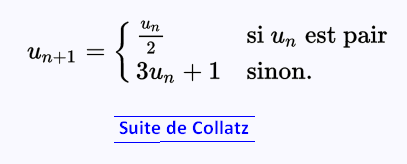
On commence par un nombre plus grand que zéro.
• s’il est pair, vous le divisez par 2;
• s’il est impair, vous le multipliez par 3 et vous ajoutez 1.
Lorsque Collatz a proposé cet algorithme, il a émit la
conjecture suivante :
On finit toujours par obtenir 1 dans la suite avec n'importe
quel nombre au départ .
Après que le nombre 1 a été atteint, la suite des valeurs (1,4,2,1,4,2…)
se répète indéfiniment en un cycle de longueur 3, appelé cycle trivial.
Cette conjecture , qui n'a pas encore été résolue,
est appelée conjecture de Syracuse ou problème de
Syracuse depuis que Helmut Hasse, un ami de Collatz, la présenta à
l'université de Syracuse (près de New York) dans les années 50.

Lothar Collatz (1910-1990) est un mathématicien allemand.
En 1937, il énonça la « conjecture de Collatz », connue également sous
le nom de conjecture de Syracuse.
|
|