Mathématiques 3: Probabilités
Fonction de répartition
Convergence en loi

1. Fonction de répartition

1.1. Définition

La fonction de répartition est utilisée en théorie des probabilités et en statistiques.

la fonction de répartition d'une variable aléatoire réelle caractérise la loi de probabilité de cette variable aléatoire réelle.

La fonction de répartition de la variable aléatoire réelle X est la fonction F_X qui à tout réel x associe

F_X(x) = P(X ≤ x)

où P(X ≤ x) représente la probabilité que la variable aléatoire réelle X prenne une valeur inférieure ou égale à x.

La probabilité que X se trouve dans l'intervalle ]a,b] est donc, si a < b:

P(a < X ≤ b ) = F_X(b) - F_X(b)

1.2. Propriétés caractéristiques de
la fonction de répartition

La fonction de répartition d'une variable aléatoire X a les propriétés caractéristiques suivantes :

• F_X est croissante ;

• Elle est partout continue à droite ;

• lim F_X(x) = 0
x → - ∞

• lim F_X(x) = 1
x → + ∞

2. Convergence en loi

Soient F1, F2, ... la suite des fonctions de répartition associées aux variables aléatoires réelles X1, X2, ..., et

F la fonction de répartition de la variable aléatoire réelle X.

Alors Fn est définie par Fn(x) = P(Xn ≤ x), et F par F(x) = P(X ≤ x).

La suite Xn converge vers X en loi, ou en distribution, si:

lim F_n(x) = F(a),
n → ∞
pour tout réel a où F est continue.

Puisque F(a) = P(X ≤ a), cela signifie que la probabilité que X appartienne à un certain intervalle est très similaire à la probabilité que Xn soit dans cet intervalle pour n suffisamment grand.

La convergence en loi est souvent notée:
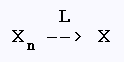