Mathématiques 3: Algèbre linéaire
Les déterminants

Déterminants

1. Définition

Le déterminant d'une matrice est la somme des produits des éléments d'une rangée (ligne ou colonne) par leurs cofacteurs respectifs. C'est le développement de Laplace du déterminant d'une matrice.

Pour une matrice m x n, on choisit une rangée, suivant laquelle nous développons, parmis les (m + n) disponibles.

2. Propriétés

• Lorsqu'on multiplie les éléments d'une rangée (ligne ou colonne) par un facteur commun, le déterminant est multiplié par ce facteur.

• Lorsqu'on ajoute à une rangée une combinaison linéaire (somme de multiples) des rangées parallèles, la valeur du déterminant ne change pas.

3. Déterminant 2 x 2

Pour calculer le déterminant d'une matrice A(2,2), on calcule la différence des produits des extrêmes et des moyens:

det(A) = a11 a22 - a21 a12

4. Technique pour calculer
le déterminant 3 x 3

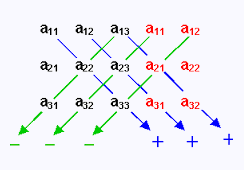
Pour calculer le déterminant d'une matrice A(3,3), on place les deux premières colonnes à droite de la matrice, puis on calcule la différence de la somme des produits :

det(A) = (a11 a22 a33 + a12 a23 a31 + a13 a21 a32) -
(a13 a22 a31 + a11 a23 a32 + a12 a21 a33)

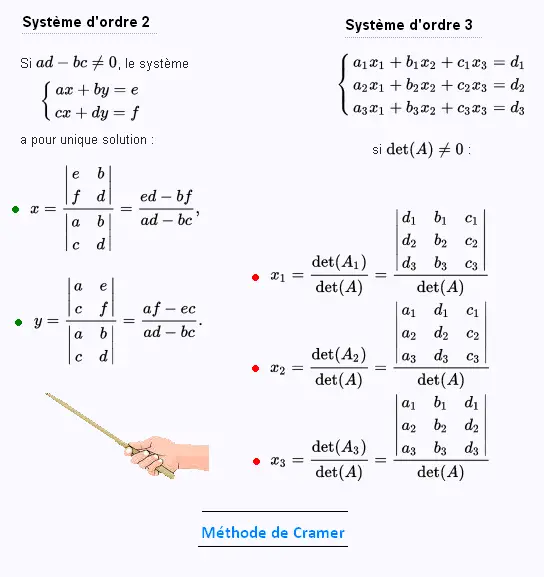
5. Règle de Cramer