Mathématiques 3: Analyse
Variation des fonctions
Fonctions de référence

Les fonctions de référence

1. La fonction identité

Définition :
La fonction identité est la fonction f définie sur R par
f(x) = x .

Propriété :
La fonction identité est strictement croissante sur R

2. La fonction carré

Définition :
La fonction carré est la fonction f définie sur R par
f(x) = x² .

Propriété :
La fonction carré est strictement décroissante sur l’intervalle ]- ∞ ; 0] et strictement croissante sur l’intervalle [0; + ∞[

3. La fonction inverse

Définition :
La fonction inverse est la fonction f définie sur R \{0} par
f(x) = 1/x .

Propriété :
La fonction inverse est strictement décroissante sur l’intervalle ]- ∞ ; 0] et strictement décroissante sur l’intervalle [0; + ∞[

4. La fonction racine carrée

Définition :
La fonction racine carrée est la fonction f définie sur [0; + ∞[ par
f(x) = √x .

Propriété :
La fonction racine carrée est strictement croissante sur l’intervalle [0; + ∞[

5. La fonction valeur absolue

Définition :
La fonction valeur absolue est la fonction f définie sur R par
f(x) = |x| .

Propriété :
La fonction valeur absolue est strictement décroissante sur l’intervalle ]- ∞ ; 0] et strictement croissante sur l’intervalle [0; + ∞[.

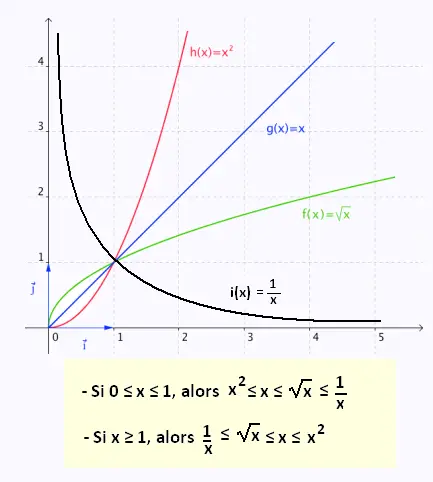
6. Ordre des fonctions de référence