Mathématiques 3: Analyse
Variation des fonctions
Limite d'une fonction en un point
Dérivabilité
Nombre dérivé
1. Limite d'une fonction en un point
Définition :
On dit que f (x) a pour limite L lorsque x tend vers xo si les valeurs
de f(x) peuvent être aussi proche de L que l'on veut pourvu que x soit suffisamment
proche de xo.
On note :
lim f(x) = L
x → xo
La limite de f(x) lorsque x tend vers xo est égale à L.
2. Dérivabilité
2.1. Coefficient directeur d'une droite
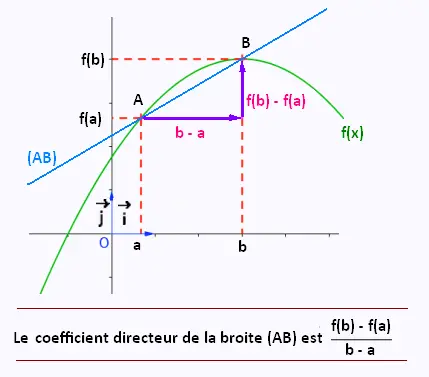
Soit une fonction f définie sur un intervalle I.
Soit deux réels a et b appartenant à I tels que a < b.
Soit A et B deux points de la courbe représentative de f d'abscisses
respectives a et b. Le coefficient directeur de la droite (AB) est égal
à :
(f(b)- f(a))/(b - a) .
2.2. Fonction dérivable
Soit une fonction f définie sur un intervalle I.
Soit un réel a appartenant à I.
Soit A et M deux points de la courbe
représentative de f d'abscisses respectives
a et a+h, avec h ≠ 0.
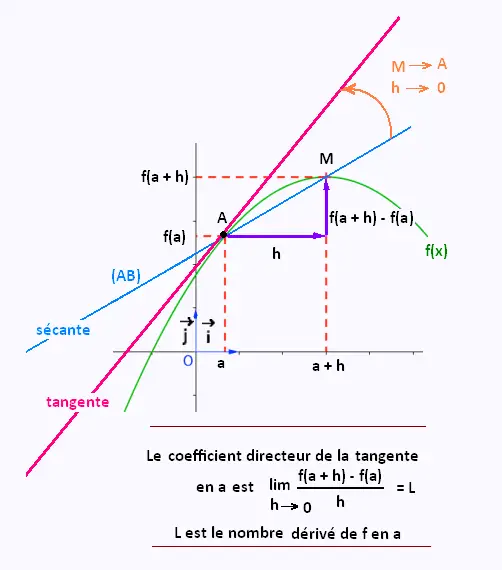
Le coefficient directeur de la droite (AM) est
égal à : (f(a + h) - f(a))/ (a + h - a) = (f(a + h) - f(a))/h .
Lorsque le point M se rapproche du point A,
le coefficient directeur de la droite (AM) est
égal à la limite de (f(a + h) - f(a))/h lorsque h
tend vers 0.
Ce coefficient directeur s'appelle le nombre
dérivé de f en a.
Définition :
La fonction f est dérivable en a s'il existe un nombre réel L, tel que :
lim (f(a + h) - f (a))/h = L .
h → 0
L est appelé le nombre dérivé de f en a.
3. Tangente à une courbe
Soit une fonction f définie sur un intervalle I, et dérivable en un nombre réel a
appartenant à I.
L est le nombre dérivé de f en a.
A est un point d'abscisse a appartenant à la courbe représentative Cf de f.
Définition :
La tangente à la courbe Cf au point A est la droite passant par A de
coefficient directeur le nombre dérivé L
Propriété :
Une équation de la tangente à la courbe Cf en A est :
y = L(x - a) + f (a)
Exemple :
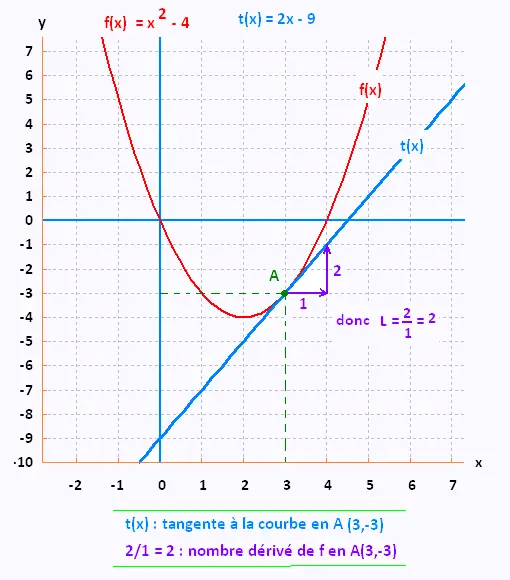
L'équation de la courbe Cf est f(x) = x2 - 4x.
Le nombre dérivé L de f en A s'obtient, après 1 unité à droite à partir du point A,
de comptant le nobre d'uniés pour rejoindre la droite tangente.
L = 2/1 = 2.
t(x) = 2(x - 3) + f (3)
D'où : f(3) = 32 - 4x3 = - 3.
Donc t(x) = 2(x - 3) - 3 = 2x - 9
L'équation de la tangente à la courbe Cf en A(3, - 3) est donc :
t(x) = 2x - 9
|