Mathématiques
1ère S
Maths 1S programme
Analyse
Géométrie
Exercices
Probabilités &
Statistiques
Applications
Suites & Séries
Calculateurs
Algèbre linéaire
© The scientific sentence. 2010
|
Mathématiques 3:
Probabilités
Résumé
1. Expérience aléatoire
Une expérience aléatoire est une expérience dont on ne connaît
pas a priori le résultat, mais dont on connaît l'ensemble des
résultats possibles.
Exemples:
- Lancer un dé.
- Choisir au hasard une boule dans une urne.
2. Issues et univers
Les résultats possibles d'une expérience aléatoire sont aussi
appelés issues.
L'ensemble des résultats possibles d'une expérience aléatoire s'appelle
l'univers ou l'univers des possibles ou l'ensemble fondamental. On le note
souvent Ω.
Exemple:
Lorsqu'on lance un dé, on a six résultats possibles : 1, 2, 3, 4, 5 ou 6.
L'univers est Ω = {1, 2, 3, 4, 5, 6}.
3. Loi de probabilité
Définition:
Soit E une expérience aléatoire et soit Ω = {e1,..., en}
l'univers de E .
On définit une loi de probabilité P sur l’univers Ω en associant
à chaque issue ei de E un nombre réel positif ou nul Pi tel que la somme
Pi+P2+...+Pn soit égale à 1.
Le nombre réel Pi s’appelle la probabilité de l'issue ei.
Notation:
On note Pi = P ({ei}) ou Pi = P (ei).
Définition:
Modéliser une expérience aléatoire E, c'est lui associer un
univers Ω et une loi de probabilité P sur Ω.
On présente souvent un modèle sous la forme d’un tableau :
| variable ei | e1 | e2 | ... | en |
| probabilité pi | p(e1) | p(e2) |
... | p(en) |
4. Equiprobabilité
Définition:
Lorsque les n issues d'une expérience aléatoire E ont toutes la même
probabilité, on dit qu'elles sont équiprobables et que la loi de
probabilité P sur Ω est équirépartie.
Exemple:
Si on lance un dé (non truqué), les résultats possibles sont
1, 2, 3, 4, 5 et 6 et chacun de ces résultats a la même probabilité
de sortir . On a Ω = {1, 2, 3, 4, 5, 6}.
| variable ei | 1 | 2 | 3 |
4 | 5 | 6 |
| probabilité pi | 1/6 | 1/6 |
1/6 | 1/6 | 1/6 | 1/6 |
5. Fréquence des issues
Soit E une expérience aléatoire et soient e1,..., en les issues
possibles.
Lorsque l'on répète plusieurs fois l'expérience E, dans les mêmes
conditions, on appelle fréquence d’apparition de l’issue ei le nombre.
fi = (nombre de fois où l'issue ei apparait)/(
npmbre de fois où l'expérienece est répétée)
6. La loi des grands nombres
On constate que lorsque l'on répète un grand nombre de fois
une même expérience, les différentes fréquences d’apparition
des issues possibles ont tendance à se stabiliser.
Ce constat est un résultat mathématique appelé «loi des grands
nombres» :
Si l'on répète k fois, dans les mêmes conditions, une expérience E, la
fréquence d'une issue de E se rapproche, lorsque k devient grand, de la
probabilité que cette issue se réalise lors d’une seule expérience.
Autrement dit :
La fréquence d’une issue tend vers sa probabilité quand le nombre
d'expériences augmente indéfiniment.
Cette loi fut énoncée pour la première fois en
1713 par Jacques Bernouilli.
Soit E une expérience d'univers.
Ω = {e1,..., en}.
Pour i 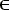 {1,...,n},
soit Pi = P ({ei}), la probabilité de l'issue ei. {1,...,n},
soit Pi = P ({ei}), la probabilité de l'issue ei.
Si on répète k fois l’expérience E dans les mêmes conditions, on note
ƒi la fréquence de l’issue ei.
Alors la loi des grands nombres dit que :
| variable ei | e1 | e2 | ... |
en |
| fréquence fi | f1 | f2 |
... | fn |
Lorsque k → +∞
| variable ei | e1 | e2 | ... |
en |
| probabilité pi | p(e1) | p(e2) |
... | p(en) |
7. Notion d'évènement
Soit E une expérience aléatoire d'univers Ω
Définition:
On appelle évènement A toute partie de l'univers Ω.
- Un évènement est élémentaire s'il est réduit à une seule issue.
- L'évènement impossible est un évènement qui ne se réalise jamais : A = Φ.
- L'évènement certain est un évènement qui se réalise toujours : A = Ω.
Remarque:
Une issue ei appartient à Ω : ei 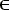 Ω. Ω.
Un évènement A est inculs dans Ω. : A = {ei}  Ω.. Ω..
Exemple:
On lance une pièce deux fois.
On note F pour face et P pour pile.
L'univers associé à cette expérience est :
Ω = {(F, F), (F, P), (P, F), (P, P)}.
L’évènement «obtenir une fois pile» s’écrit
{(F, P), (P, F)}.
L’évènement «obtenir deux fois face» s’écrit
{(F, F)}.
C'est un évènement élémentaire puisqu'il ne contient qu'une
seule issue .
8. Probabilité d'un évènement
Définition:
La probabilité d'un évènement A non vide est le nombre réel noté P(A) qui est égal
à la somme des probabilités des issues qui le réalisent.
Propriété:
P (Ω) = 1
P (Φ) = 0
Pour tout évènement A, 0 ≤ P(A) ≤ 1
Propriété:
Soit E une expérience aléatoire d'univers associé Ω = {e1,....,en}.
Si la loi de probabilité est équirépartie et si A est un évènement réalisé
pour k issues, alors :
P(A) = k /n = (nombre d'issues favorables à A)/(nombre total d'issues)
Exemple:
On lance deux fois une pièce bien équilibrée et on note F pour face et P pour pile.
L'univers associé est :
Ω = {(F, F), (F, P), (P, F), (P, P)}
et la loi de probabilité est équirépartie.
| variable ei | (F,F) | (F,P) |
(P,F) | (P,P) |
| probabilité pi | 1/4 | 1/4 |
1/4 | 1/4 |
Soient A l'évènement «obtenir une fois pile» et
B l'évènement «obtenir deux fois face».
On a
A = {(F, P), (P, F)}
et
B = {(F, F)}.
P(A) = (nombre d'issues qui réalisent A)/(
nombre d'issues total) = 2/4 = 1/2
P(B) = (nombre d'issues qui réalisent B)/(
nombre d'issues total) = 1/4
9. Opérations sur les évènements
Définitions:
Soient A et B deux évènements.
• A B est réalisé lorsque A et B sont tous les deux réalisés. B est réalisé lorsque A et B sont tous les deux réalisés.
• A B est réalisé lorsque A ou B (au moins l'un des deux) est réalisé. B est réalisé lorsque A ou B (au moins l'un des deux) est réalisé.
•  est l'évènement contraire de A.
Il est réalisé lorsque A ne l'est pas. est l'évènement contraire de A.
Il est réalisé lorsque A ne l'est pas.
- A et B sont dits incompatibles ou disjoints s'ils ne peuvent se réaliser
simultanément.
|
|

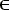 {1,...,n},
soit Pi = P ({ei}), la probabilité de l'issue ei.
{1,...,n},
soit Pi = P ({ei}), la probabilité de l'issue ei.
 Ω..
Ω..
 B est réalisé lorsque A et B sont tous les deux réalisés.
B est réalisé lorsque A et B sont tous les deux réalisés.
 B est réalisé lorsque A ou B (au moins l'un des deux) est réalisé.
B est réalisé lorsque A ou B (au moins l'un des deux) est réalisé.
 est l'évènement contraire de A.
Il est réalisé lorsque A ne l'est pas.
est l'évènement contraire de A.
Il est réalisé lorsque A ne l'est pas.
