Mathématiques
1ère S
Maths 1S programme
Analyse
Géométrie
Exercices
Probabilités &
Statistiques
Applications
Suites & Séries
Calculateurs
Algèbre linéaire
© The scientific sentence. 2010
|
Mathématiques 3: Algèbre
Suites e séries
La suite de Fibonacci
Complexité d'un algorithme
Suite de Fibonacci
1. Définition
On sait que le terme de rang n de la suite de de
Finonacci est :
fibonacci(n) = fibonacci(n - 1) + fibonacci(n - 2)
C'est à dire la valeur de l'avant dernier + celle de
l'antépénultième.
2. Complexité d'un algorithme
Les principaux objectifs des calculs de complexité sont:
• pouvoir prévoir le temps d'exécution d'un algorithme,
• pouvoir comparer deux algorithmes réalisant le même traitement
Exemples:
Si on lance le calcul de fibonacci de 100, combien de temps
faudra t-il attendre le résultat?
Les temps d’exécution d'un programme dépendent beaucoup des processeurs utilisés.
Ils dépendent aussi de l'algorithme utilisé.
3. Algorithme récursif pour fibonacci(5)
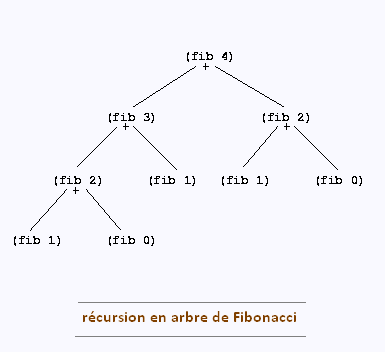
On veut calculer fibo(5).
Tout d’abord fibo(5) est remplacé par fibo(3) +
fibonacci(4). Puisque ces deux nombres sont inconnus, la procédure récursive les remplace
par leur définition pour obtenir fibo(1)+fibo(2)+fibo(2)+fibo(3). Enfin, puisque
fibo(3) est inconnu, lui aussi est remplacé par sa définition et ainsi de suite ...
Avec cette version récursive, le processus de calcul de fibonacci(n) prend
un temps qui croît de façon exponentielle avec n.
4. Fibonacci d'un nombre plus grand
Nous avons:
fibonacci de 10 = 55
fibonacci de 50 = 12,586,269,025
fibonacci de 100 = 354,224,848,179,261,915,075
fibonacci de 1000 =
4346655768693745643568852767504062580256466051737178040248172908953655
5417949051890403879840079255169295922593080322634775209689623239873322
471161642996440906533187938298969649928516003704476137795166849228875
et comporte 209 chiffres.
fibonacci de 3000 =
41061588630797126033356837871926710522012510863736925240888543092690
55842741134037313304916608500445608300368357069422745885693621454765
02674373045446852160486606292497360503469773453733196887405847255290
08204908690751262205905454219588975803110922267084927479385953913331
83712447955431476110732762400667379340851917318109932017067768389347
66764778739502174470268627820918553842225858306408301661862900358266
85723821023580250435195147299791967652400478423637645334726836415264
83462458405732142414199379172429186026398100978669423920154046201538
18671425739835074851396421139982713640679581178458198658692285968043
243656709796000
fibonacci de 4782 contient 1000 chiffres.
Voici, en langage C++, le code source d'un programme de calcul
du nième terme de la suite de Fibonacci.
Dans ce programme, on peut utliser soit yun algorithme récursif,
soit un algorithme itératif.
1. Calcul récursif:
int fibonacci(int n)
{
if((n==1)||(n==0))
{
return(n);
}
else
{
return(fibonacci(n-1)+ fibonacci(n-2));
}
}
2. Calcul itératif:
int fibonacci(int n) {
int u = 0;
int v = 1;
int i, t;
for(i = 2; i <= n; i++) {
t = u + v;
u = v;
v = t;
}
return v;
}
Lorsque l'efficacité en temps d'exécution des programmes est
en jeu, l'ecriture de l'algorthme est très importante.
L'un des algorithmes les plus consommateurs de temps est
l'algorithme récursif.
Les temps d'exécution des versions itérative et récursive:
Le calcul itératif d'un fibonacci ecrit en php ou C++ , ou Python avec
n = 50 et n = 55 sur un actuel Intel ou AMD prend quelques
millisecondes, alors que le calcul récursif necéssite des minutes.
Au delà ce sont des heurs ou des jours de calculs.
fibonacci(5) nécessite pas moins de 9 appels récursifs et
fibonacci(50) plus de 25 milliards!
La compléxité de l'algorithme récursif est exponentielle.
On lui préfère donc celle linéaire de la vérsion itérative.

|
|