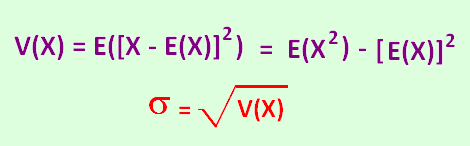Mathématiques 3:
Probabilités et Statistiques
Variable aléatoire
Loi de probabilité
Espérance mathématique
Variance et écart-type

1. Variable aléatoire

Définition:

Une variable aléatoire X est l'ensemble des valeurs réelles correspondant aux résultats possibles d'une expérience aléatoire.

X = {x1, x2, x3, ..., xn}

On la note aussi X(Ω), où &Omeag; est l'ensemble des résultats possibles.

Exemple:

On lance deux dés , c'est l'expérience aléatoire.

On note la somme des faces obtenues, c'est à dire la variable aléatoire:

X = {2, 3, ..., 12}

2. Loi de probabilité

Définition :

À chaque variable xi correspond une probabilité. On forme alors une fonction de répartition des valeurs ou une loi de probabilité de la variable aléatoire, ensemble :

{pi| pi = p(xi) avec Σpi = 1}

variable	x1	x2	...	xn
probabilité	p(x1)	p(x2)	...	p(xn)

Exemple:

On lance deux dés. On considère la variable aléatoire X telle que pour chaque issue, on additionne les valeurs des faces. Voici la loi de probabilité de cette variable:

Issues : Ω    Card(Ω) = 36	X(Ω)	P(X)/ 36
(1,1)	2	1
(1,2),(2,1)	3	2
(1,3), (2,2), (3,1)	4	3
(1,4), (2,3), (3,2), (4,1)	5	4
(1,5), (2,4), (3,3), (4,2) (5,1)	6	5
(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)	7	6
(2,6), (3,5), (4,4), (5,3), (6,2)	8	5
(3,6), (4,5), (5,4), (6,3)	9	4
(4,6), (5,5), (6,4)	10	3
(6,5), (5,6)	11	2
(6,6)	12	1

3. L'Éspérance

Définition :

L' espérance mathématique d'une variable aléatoire réelle est la valeur que l'on espère ou que l'on s'attend à trouver, en moyenne, si l'on répète un grand nombre de fois la même expérience aléatoire.

Pour une variable aléatoire X, elle se note E(X)} et se lit «espérance de X».

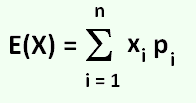
Théoriquement l' espérance mathématique correspond à une moyenne pondérée des valeurs que peut prendre cette variable.

Il s'agit d'une moyenne pondérée par les probabilités d'apparition de chaque valeur.

Dans un contexte de jeux de hasard:

• Lorsque l’espérance mathématique est égale à 0 (E = 0), on dit que le jeu est équitable.

• Lorsque l’espérance mathématique est négative (E < 0), cela signifie qu’en moyenne, le joueur perdra de l’argent à chaque essai.

• Lorsque l’espérance mathématique est positive (E > 0), cela signifie qu’en moyenne, le joueur gagnera de l’argent à chaque essai. Ce montant gagné à chaque essai sera en moyenne égal à l’espérance mathématique.

Exemple:

Considérons le jeu des deux dés

4. La variance et l'écart-type

Définition:

La variance et l'écart-type mesurent la dispersion autour de l'espérance (ou moyenne).



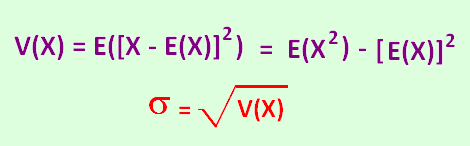
Exemple:

Considérons le jeu des deux dés