Mathématiques 3: Géometrie
Vecteurs et droites
1. Colinéarité de deux vecteurs
• Définition :
Deux vecteurs non nuls et et sont colinéaires signifie qu’ils ont même direction
c’est-à-dire qu’il existe un nombre réel k tel que
sont colinéaires signifie qu’ils ont même direction
c’est-à-dire qu’il existe un nombre réel k tel que
 = k = k
• Critère de colinéarité :
Soit  et et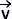 deux vecteurs de coordonnées (x1, y1) et (x2, y2)
dans un repère (O,
deux vecteurs de coordonnées (x1, y1) et (x2, y2)
dans un repère (O,  , ,
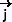 , ,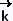 ). ).
Les vecteurs  et et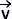 sont colinéaires si leur
déterminant det( sont colinéaires si leur
déterminant det(  , ,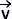 ) est nul ,
c'est à dire
x1 y2 - y1 x2 = 0 . ) est nul ,
c'est à dire
x1 y2 - y1 x2 = 0 .
2. Equations de droite
2.1. Vecteur directeur d'une droite
• Définition :
D est une droite du plan.
On appelle vecteur directeur de D tout vecteur non nul  qui possède la même direction que la droite D.
qui possède la même direction que la droite D.
2.2. Equation cartésienne d'une droite
• Théorème et définition :
Toute droite D admet une équation de la forme ax + by + c = 0
avec a et b non nul.
Cette équation est appelée équation cartésienne de la droite D.
Un vecteur directeur de D est 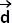 (- b ; a). (- b ; a).
2.3. Equation cartésienne et équation réduite
Si b ≠ 0 , alors l'équation cartésienne ax + by + c = 0 de la droite D peut être ramenée
à une équation réduite y = - (a/b) x - c/b.
Le coefficient directeur de D est - a/b, son ordonnée à l'origine est - c/b.
Un vecteur directeur de D est (1, - a/b).
2.4. Parallélisme de droites
Propriété :
Les droites d'équation ax + by + c = 0 et
a' x + b' y + c' = 0 sont parallèles si
le déterminant de leurs vecteurs directeurs respectifs (- b, a) et (- b', a')
est nul, c'est à dire ab'- a'b = 0
3. Décomposition d'un vecteur
Définition :
On appelle base du plan tout couple de vecteurs non colinéaires.
Propriété :
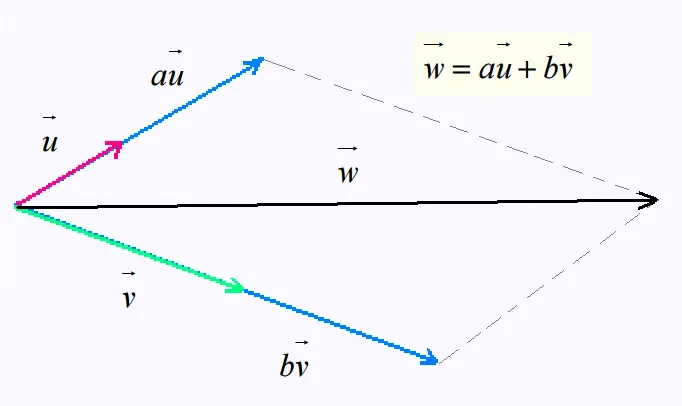
Soit ( ; ;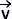 ) une base du plan.
Pour tout vecteur ) une base du plan.
Pour tout vecteur 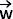 , il existe un unique couple de
nombres réels (a ; b) tel que : , il existe un unique couple de
nombres réels (a ; b) tel que : 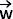 = a = a  +
b +
b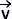 . .
|