Mathématiques
1ère S
Maths 1S programme
Analyse
Géométrie
Exercices
Probabilités &
Statistiques
Applications
Suites & Séries
Calculateurs
Algèbre linéaire
© The scientific sentence. 2010
|
Mathématiques 3: Algèbre linéaire
Valeurs propres et vecteurs propres
Valeurs propres et vecteurs propres
1. Définitions
Soit A une matrice carrée de format n x n. On dit qu'un nombre λ est une
valeur propre de A s'il existe un vecteur non-nul X à n
composantes tel que A X = λ X. Dans ce cas, on dit que X
est un vecteur propre de A correspondant à la valeur propre λ.
Étant donnée une matrice carrée A de format n x n, les valeurs propres de A
sont les solutions de l’équation:
det(A - λ I) = 0
où det(A - λ I) représente le déterminant de la matrice A - λ I
et I est la matrice identité de même format que A.
En résolvant cette équation, on trouve les n valeurs propres λ
de A d'ordre n x n.
Comment trouve-t-on alors les vecteurs propres de A?
Si X est un vecteur propre de A correspondant à la valeur propre λ,
alors A X = λ X.
C'est à dire (A - λ I)X = 0. Ceci implique que chaque vecteur
propre X de A est une solution du système homogène (A - λ I) X = 0,
de n equations à n inconnues.
On définit alors l'espace propre Eλ
correspondant à la valeur propre λ de A comme étant l'ensemble
de tous les vecteurs propres correspondant à λ y
compris le vecteur nul.
En d’autres termes, Eλ représente
l'ensemble de solutions du système (A - λI) X = 0.
3. Exemple 1: Suite de Fibonacci
Voici la suite de Fibonacci:
f0 = 1, f1 = 1, f2 = 2, f3 = 3, f4 = 5,...
En général:
fn = fn-1 + fn-2
Construisons le vecteur
Vn = (fn+1, fn)
Vn+1 = (fn+2, fn+1) =
F (fn+1, fn) = F Vn
avec la matrice F, d'ordre 2 x 2 égale à:
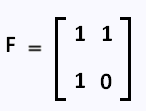
• Ecrivons L'équation aux valeurs propres :
det(F - λI) = (1 - λ) x (-λ) - 1 = 0
ou λ2 - λ - 1 = 0 , de solutions
λ1 = (1 + √5)/2
λ2 = (1 - √5)/2
• Calculons les vecteurs propres:
(F - λI) X = 0 , avec X = (x, y), donne
(1 - λ) x + y = 0
x - λ y = 0
On peut prendre y = 1 et donc x = λ:
X = (λ, 1)
Les deux vecteurs propres sont:
X1 = ((1 + √5)/2, 1)
X2 = ((1 - √5)/2, 1)
Qui sont respectivement des bases
de l’espace propre Eλ1 et
Eλ2.
Les vecteurs propres X1 et X2 forment la matrice
de conjugaison P de la matrice F .
Voici la matrice D, P, et P-1:
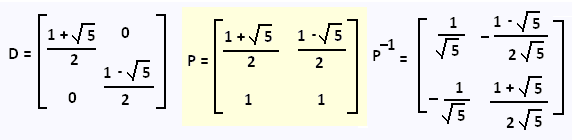
Décomposons la matrice F selon:
F = P D P-1
, donc:
Fn = P Dn P-1
, avec
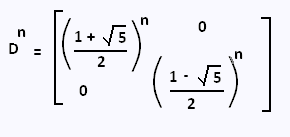
Après avoir effectué les multiplications, on prend la deuxième composante du vecteur résultant. C'est le nième terme de la
suite de Fibonacci:
Mantenant, puisque
Vn = F Vn-1 = F2 Vn-2 = ... =
Fn V0
Avec
V0 = (f1, f0) = (1,1)
et
Vn = (fn+1, fn)
fn = (1/√5){[(1 + √)/2]n+1 - [(1 - √5)/2]n+1}
On peut donc calculer le 100ième terme de la suite de Fibonacci :
f100 = (1/√5){[(1 + √)/2]101 - [(1 - √5)/2]101}
On peut négliger le deuxième terme :
[(1 - √5)/2]101 pour obtenir
une valeur de 573 147 844 013 817 084 101.
f100 = 573 147 844 013 817 084 101
On rappelle que le nombre φ = (1 + √5)/2 est appelé nombre d’or .
2. Exemple 2: Deux masses liées par
trois ressorts
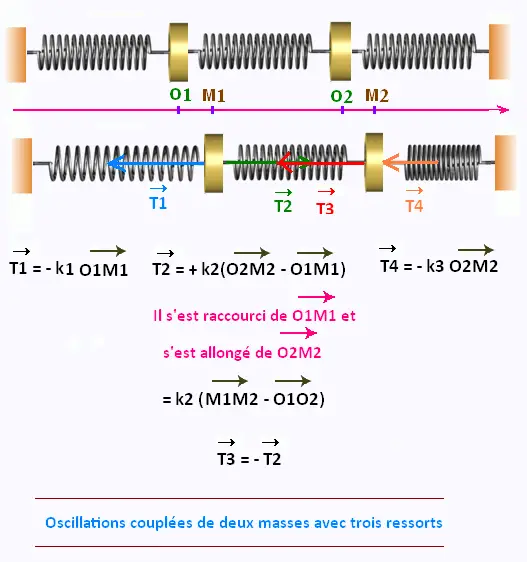
On considère deux blocs de masses respectives m1 et m2 liés l'un à l'autre par un ressort de constante de raideur k2 . Le bloc de masse m1 est lié à un point d'ancrage fixe par l'intermédiaire d'un ressort de constante de raideur k1 et, à l'autre extrémité du système, le bloc de masse m2 est lié à un point d'ancrage fixe par l'intermédiaire d'un ressort de constante de raideur k3.
La masse des ressorts est négligeable et on suppose que l'amplitude de déplacement des deux blocs est toujours suffisamment faible pour que la loi de Hooke soit vérifiée.
Finalement, tous les frottements sont considérés comme négligeables.
On considère que les blocs sont de masse identique de sorte que
m1 = m2 et et que les ressorts ont la même constante de raideur k1 = k2 = k3,
Ecrivons:
O1M1 = x1
O2M2 = x2
m d2x1/dt2 = T2 - T1 = kx2 - 2kx1
m d2x2/dt2 = - T3 - T4 =
- 2kx2 + kx1
Soit
m d2x1/dt2 = - 2k x1 + k x2
m d2x2/dt2 = k x1 - 2k x2
Sous forme vectorielle, ce système s'écrit :
d2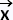 /dt2 =
R /dt2 =
R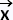 ,
Avec
,
Avec
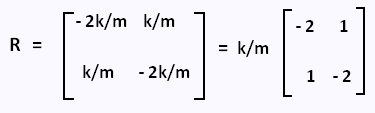
et 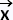 = (x1(t), x2(t)) = (x1(t), x2(t))
On cherche alors une solution réelle de la forme
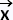 = = 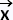 o exp{iωt} . o exp{iωt} .
En dérivant deux fois cette solution par rapport au temps et en remplaçant dans l'équation vectorielle, il vient :
ω2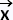 o = R o = R
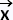 o o
En posant λ = ω2 , on a alors un problème aux valeurs propres
R 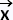 o = λ o = λ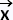 o o
avec λ valeur propre de R et 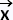 o vecteur propre de R. o vecteur propre de R.
Pour déterminer les valeurs propres, il faut résoudre :
det(R = λI) = 0
Ce qui conduit à l'équation:
λ2 + 4(k/m) λ + 3(k/m)2 = 0
Une équation du second degré avec deux solutions possibles ,
valeurs propres de R:
λ1 = - k/m
λ2 = - 3k/m
Pour déterminer les vecteurs propres,
il faut résoudre :
R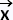 1 = λ1 1 = λ1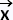 1
et 1
et
R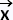 2 = λ2 2 = λ2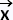 2 2
Avec
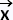 1 = (x1, y1) , et 1 = (x1, y1) , et
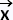 2 = (x2, y2). 2 = (x2, y2).
• Pour λ1 , on trouve x1 = y1.
On choisit
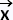 1 = (1, 1) 1 = (1, 1)
• Pour λ2 , on trouve x2 = - y2.
On choisit
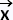 2 = (1, - 1) 2 = (1, - 1)
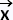 1 = (1, 1): le vecteur
propre associé à 1 = (1, 1): le vecteur
propre associé à
la valeur propre λ1 = - k/m
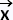 2 = (1, - 1): le vecteur propre associé à 2 = (1, - 1): le vecteur propre associé à
la valeur propre λ2 = - 3k/m
|
|