Mathématiques: GEOMETRIE PLANE
Exercice 1
(C) est un cercle de 2.5 cm de rayon. Le segment [AB] est un diamètre de ce cercle. M est un point de ce cercle tel que
AM = 3 cm.
1) Construire la figure.
2) Démontrer que le triangle ABM est rectangle.
3) Calculer la longueur MB.
Exercice 2
ABC est un triangle rectangle en A tel que
AB = 7 cm et BC = 12 cm.
1) Faire une figure à main levée.
2) Calculer AC. On donnera la valeur exacte.
3) Déterminer la mesure de l’angle ∠CBA au degré près.
Exercice 3
On considère un triangle ABC tel que AB = 60 mm, BG = 75 mm et CA = 45 mm.
1) Construire le triangle ABC.
2) Montrer que le triangle ABC est rectangle et préciser en quel point.
3) Construire le point M milieu de [AB] et construire la droite parallèle à [AC] passant par M ; elle coupe [BC] en N.
4) Montrer que N est le milieu de [BC].
Exercice 4
On donne:
Deux droites parallèles (AB) et (CD) , à l'intérieur desquelles deux droites (AC) et (BD) sécantes au point O.
1) Tracer une figuregure (avec les quatres droites selon les
mesures suivantes:
OA = 7.5cm ; OB = 4 cm ;
OC = 3 cm ; et OD = 1.6 cm.
2) Montrer que les droites (DC) et (AB) sont parallèles.
3) Sachant que DC = 5 cm, calculer AB.
Exercice 5
On considère un triangle ABC tel que AB = 6 cm, BC = 7.5 cm et AC = 4.5 cm.
1) Construire le triangle ABC.
2) Montrer que le triangle ABC est rectangle et préciser en quel point.
3) Construire le point M milieu de [AB] et construire la droite parallèle à [AC] passant par M ; elle coupe [BC] en N.
4) Montrer que N est le milieu de [BC].
Exercice 6
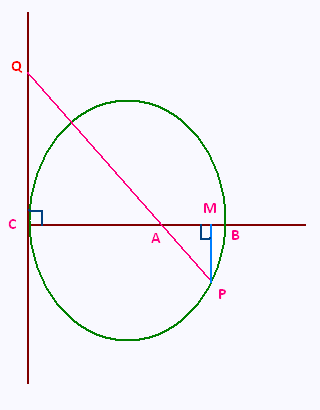
On considère un cercle de centre A et de rayon 5 cm.
Soit [BC] un de ses diamètres, M le point du segment [AB]
tel que AM = 4 cm et P un point du cercle tel que
MP = 3 cm.
La figure n’est pas en vraie grandeur.
1) Démontrer que le triangle AMP est rectangle en M.
2) On trace la tangente au cercle en C ; cette droite
coupe la droite (AP) en Q.
a) Démontrer que les droites (CQ) et (MP) sont parallèles.
b) Calculer la longueur AQ.
Exercice 7
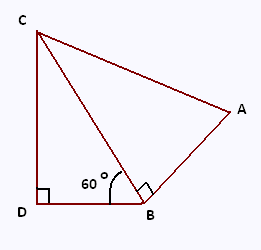
On donne:
BD = 4 cm ; BA = 6 cm et mes(∠DBC) = 60o.
On ne demande pas de faire une figure en vraie grandeur.
1) Montrer que BC = 8 cm.
2) Calculer CD.
Donner la valeur arrondie au dixième.
3) Calculer AC.
4) Quelle est la valeur de tan (∠BAC) ?
5) En déduire la valeur arrondie au degré de ∠BAC.
Exercice 8
On considère un cercle de centre O et de diamètre [BC] tel que BC = 8 cm. On place sur ce cercle un point A tel que
BA = 4 cm.
1) Faire une figure en vraie grandeur.
2) a) Démontrer que le triangle ABC est rectangle en A.
b) Calculer la valeur exacte de la longueur AC.Donner la valeur arrondie de AC au millimètre près.
c) Déterminer la mesure de l'angle .
3) On construit le point E symétrique du point B par rapport au point A. Quelle est la nature du triangle BEC ?
Justifier.
Exercice 9
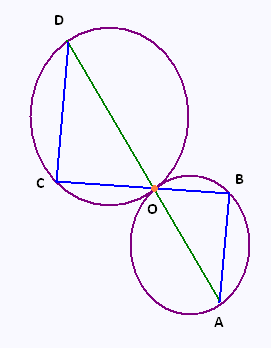
La figure ci-contre n’est pas en vraie grandeur . Elle n'est pas
à reproduire.
Les points D, O, et A sont alignés ainsi que les points C, O, et B.
Les segments [OD] et [OA] sont des diamètres des deux cercles
tracés.
On donne : OD = 7.5 cm et OA = 4.5 cm.
1) Prouver que le triangle OCD est rectangle en C, et que
le triangle OAB est rectangle B.
2) Justifier que les droites (CD) et (AB) sont parallèles.
3) Dans le cas où OC = 5 cm, calculer la distance OA.
Justifier.
Exercice 10
L’unité de longueur est le centimètre.
ABC est un triangle tel que AB = 9 ; AC = 15 ; BC = 12.
1) a) Démontrer que ABC est rectangle en B.
b) Tracer en vraie grandeur le triangle ABC.
2) M est le point du segment [AB] tel que AM = 3.
N est le point du segment [AC] tel que AN = 5.
a) Placer les points M et N sur la figure.
b) Démontrer que la droite (MN) est parallèle à la droite (BC).
3) Calculer l’aire du triangle AMN.
Exercice 11
1) Construire un triangle ABC rectangle en A et tel que AC = 6 cm, BC = 7.5 cm.
2) Montrer par le calcul que AB = 4.5 cm.
3) Sur la demi-droite [AC), placer le point M tel que AM = 10.8 cm. Sur la demi-droite [AB), placer le point N tel que
AN = 8.1 cm.
a) Montrer que les droites (BC) et (MN) sont parallèles.
b) Calculer MN.
Exercice 12
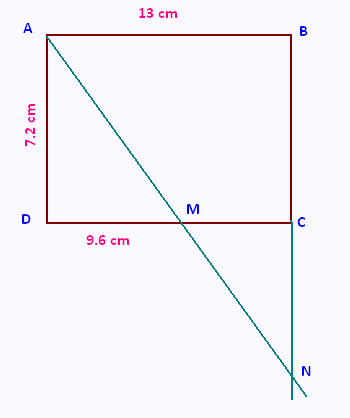
Sur la figure ci-contre, qui n’est pas en vraie grandeur, le quadrilatère ABCD est un rectangle avec AB = 13 cm et
AD = 7.2 cm.
Le point M est sur le segment [DC] tel que DM = 9.6 cm.
N est le point d’intersection des droites (AM) et (BC).
1) Démontrer que la longueur MC est égale à 3.4 cm.
2) Calculer la longueur AM.
3) Calculer la longueur CN.
Exercice 13
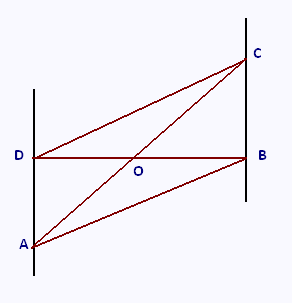
Les points D, O, B d’une part et les points A, O, C d’autre
part sont alignés dans cet ordre.
OC = 6 cm : OA = 9 cm ; OD = 5.4 cm et OB = 3.6 cm.
1) Les droites (AD) et (BC) sont-elles parallèles ? Justifier.
2) On suppose que BC = 4.8 cm. Le triangle OBC est-il rectangle ? Justifier.
3) En utilisant le théorème de Thalès, calculer AD.
4) On admettra que les droites (AD) et (DB) sont perpendiculaires.
Quelle est l’aire du quadrilatère ABCD ? Justifier.
Exercice 14
L’unité de longueur est le centimètre.
ABC est un triangle tel que : AB = 16 cm, AC = 14 cm et BC = 8 cm.
1) a) Tracer en vraie grandeur le triangle ABC.
b) Le triangle ABC est-il rectangle ? Justifier.
2)
On not AB = c, BC = a, AC = b et p le périmètre du triangle.
L’aire S du triangle est donnée par la formule de Héron:
Calculer à l’aide de cette formule l’aire du triangle ABC.
Donner le résultat arrondi au cm2 près.
Exercice 15
On considère un triangle isocèle ABC tel que
AB = AC = 4 cm.
E est le symétrique de B par rapport à A.
1 : mesure 33o.
a) Construire la figure en vraie grandeur.
b) Quelle est la nature du triangle BCE ? Justifier.
c) Prouver que l’angle CAE mesure 66o.
2 : est aigu et est quelconque.
A-t-on toujours CAE = 2 CBA ? Justifier.
Exercice 16
ABC est un triangle rectangle en B tel que AB = 8 cm
et l'angle ∠ACB mesure 40o.
1) Faire une figure à main levée.
2) Calculer AC On arrondira la valeur au mm près.
Exercice 17
Soit ABC un triangle tel que :
AB = 10.4 cm ; AC = 9.6 cm ; BC = 4 cm.
1) Faire une figure qui sera complétée au fur et à mesure.
2) Démontrer que le triangle ABC est un triangle rectangle.
3) Soit D le point du segment [AB] tel que AD = 7.8 cm.
Le cercle (C ) de diamètre [AD] recoupe le segment [AC] en E.
Préciser la nature du triangle AED.
Démontrer que les droites (BC) et (DE) sont parallèles.
4) Calculer DE.
Exercice 18
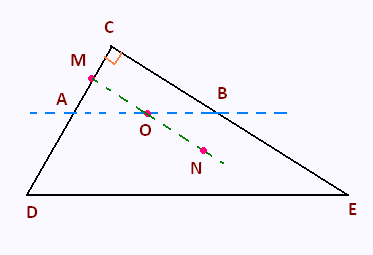
• CDE est un triangle rectangle en C.
• A appartient au segment [CD], B appartient au segment
[CE] et la droite (AB) est parallèle à la droite (DE).
• Le point M est le milieu du segment [AC] et le point O est
le milieu de [AB].
• Le point N est le symétrique de M par rapport à O.
• DE = 12 cm ; AB = 4.5 cm et AC = 1.8 cm.
1) Quelle est la nature du quadrilatère AMBN ?
2) Montrer que la droite (MO) est parallèle à la droite (CB).
3) Calculer la longueur CD.
4) Calculer une valeur approchée au degré près de l’angle BAC.
Exercice 19
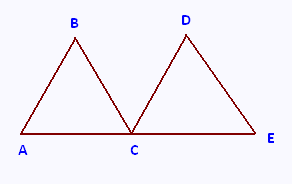
ABC et CDE sont deux triangles équilatéraux de côté 4 cm.
Les points A, C et E sont alignés.
1) Faire une figure exacte, en respectant les longueurs
données, et la compléter au fur et à mesure.
2) Prouver que les points A, B, D, E sont sur un même cercle
Indiquez le centre et le rayon de ce cercle.
3) Prouvez que ABE est un triangle rectangle.
4) Calculez les mesures des côtés et des angles du triangle
ABE.
5) Prouvez que BCD est un triangle équilatéral.
Exercice 20
On considère un cercle de centre O et de diamètre 8 cm.
A et B sont deux points de diamétralement opposés,
M est un point du cercle tel que BM = 4 cm.
1) Faire une figure à main levée.
2) Préciser la nature du triangle ABM. Justifier.
3) Préciser la nature du triangle OBM. Justifier.
4) On appelle N le symétrique de M par rapport à la
droite (AB).
Démontrer que le quadrilatère NOMB est
un losange.
Exercice 21
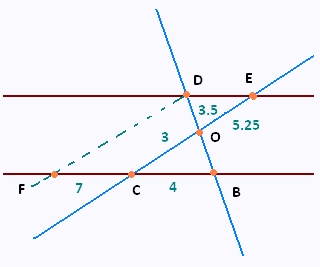
la figure n'est pas à l'échelle.
– les points F, C et B sont alignés dans cet ordre ;
– les segments [CE] et [BD] se coupent au point O;
– les droites (BC) et (DE) sont parallèles.
On donne les longueurs :
BC = 4 ; CO = 3 ; OD = 3.5 ;
FC = 7 ; OE = 5.25.
1) Démontrer que AB = 2.
2) Démontrer que les droites (OC) et (DF) sont parallèles.
Exercice 22
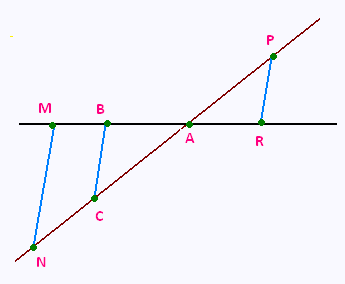
On précisera pour chacune des deux questions de
cet exercice la propriété utilisée.
La figure ci-contre n’est pas représentée en vraie grandeur.
Les droites (BC) et (MN) sont parallèles.
On donne :
AB = 2.4 cm ; AC = 5.2 cm ;
AN = 7.8 cm et MN = 4.5 cm.
1) Calculer les longueurs AM et BC.
2) Sachant que AP = 2.6 cm et AR = 1.2 cm, montrer que les
droites (PR) et (BC) sont parallèles.
Exercice 23
Soient un cercle (C) de centre O et de rayon 5 cm.
[AB] est un diamètre de ce cercle et M est un point de (C) tel que BM = 4.2 cm.
1) Faire une figure.
2) Montrer que ABM est un triangle rectangle.
3) Quelles sont les mesures, arrondies au degré, des angles MBA et MOA ?
Exercice 24
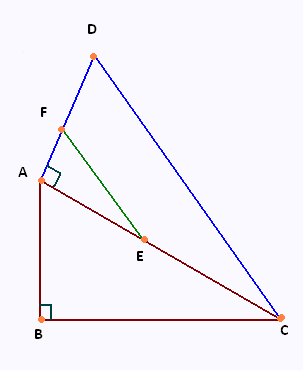
Sur la figure ci-contre:
• Les angles ∠DAC et ∠ABC sont droits,
• L'angle ∠CAB mesure 50o,
• AD = 5 cm, et AC = 7 cm.
1) Calculer BC, puis en donner la valeur arrondie au mm près.
2) Calculer DC. On donnera sa valeur exacte.
3) Calculer la mesure de l’angle ∠ CDA en donnant sa valeur arrondie à un degré près.
4) Les droites (EF) et (CD) sont parallèles et AE = 2.5 cm.
Calculer AF.
On donnera
la valeur exacte puis la valeur arrondie au mm près.
Exercice 25
ABCD est un parallélogramme de centre O, tel que AC = 12 cm,
BD = 6.4 cm et AB = 6.8 cm.
1) Faire une figure à main levée.
2) Construire ABCD en vraie grandeur.
3) Conjecturer la nature précise du quadrilatère ABCD.
4) Prouver que le résultat observé à la question 3 est vrai.
Exercice 26
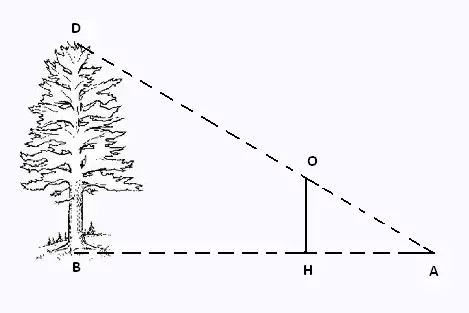
On veut trouver la hauteur BD d’un arbre.
On dispose des renseignements suivants :
HA = 1m ; BH = 5 m et OH = 0.9 m.
Les points A, H et B sont alignés, ainsi que les points
O, A et D.
Les angles ∠OHA et ∠DBA sont droits.
1) Démontrer que les droites (OH) et (BD) sont parallèles.
2) Calculer la hauteur de l’arbre.
Exercice 27
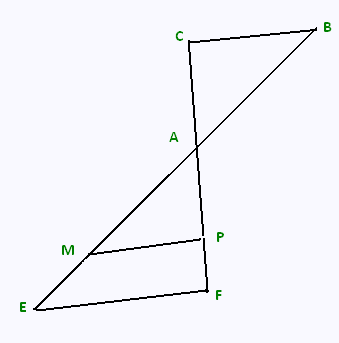
L’unité est le millimètre. La figure ci-contre n’est pas à
l’échelle.
On ne demande pas de refaire cette figure.
Les points E, M, A, B sont alignés dans cet ordre.
Les points F, P, A, C sont alignés dans cet ordre.
Les droites (EF) et (MP) sont parallèles.
AM = 60 ; MP = 48 ; AP = 36 ;
EF = 60 ; AC = 45 ; AB = 75.
1) Démontrer que le triangle AMP est un triangle rectangle.
2) Calculer AE et en déduire la longueur ME . Justifier les calculs.
3) Démontrer que les droites (MP) et (BC) sont parallèles.
4) Démontrer que les angles ∠ABC et ∠AMP sont égaux.
Exercice 28
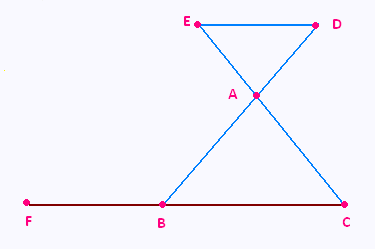
La figure suivante n’est pas réalisée en vraie grandeur.
L’unité de longueur est le centimètre.
On donne AB = 8 ; BC = 9 ; AC = 6 ; AE = 4.
1) Les droites (DE) et (BC) sont parallèles.
Calculer AD. On donnera sa valeur exacte puis sa valeur arrondie au dixième de centimètre.
2) Soit F le point tel que C, B et F sont alignés dans cet
ordre, avec BF = 6.
3) Démonter que les droites (EF) et (AB) sont parallèles.
Exercice 29
l’unité de longueur est le centimètre.
ABC est un triangle rectangle en C.
D est un point du segment [AB].
E est un point du segment [AC].
On donne :
AC = 6 ; BC = 4.5 ; AD = 4 ;
(DE) // (BC).
1) Faire une figure à main levée.
2) Prouver que AB = 7.5.
3) Calculer AE.
4) a) Calculer le cosinus de l’angle
b) En déduire la mesure, arrondie au degré, de l’angle A.
Exercice 30
On considère deux droites (ED) et (AB), à
l'intérieur desquellles les droites (EB) et (DA)
sont sécantes en C.
On donne :
CE = 5 , CD = 12 , CA = 18 ,
CB = 7.5 , AB = 19.5.
1) Faire une figure à main levée.
2) Montrer que les droites (ED) et (AB) sont parallèles.
3) Montrer que ED = 13.
4) Montrer que le triangle CED est un triangle rectangle.
5) Calculer tan(∠DEC) puis en déduire la valeur arrondie au degré de la mesure de l’angle ∠DEC.
Exercice 31
L’unité de longueur est le centimètre.
ABC est un triangle tel que
AB = 6.4 ; BC = 8 et AC = 4.8.
1) Construire la figure en vraie grandeur.
2) Démontrer que le triangle ABC est rectangle en A.
3) Calculer la valeur arrondie au degré près de la mesure de l’angle ∠ABC.
4) M est le point du segment [AB] tel que BM = 4 et N est le point du segment [BC] tel que BN = 5.
a) Démontrer que les droites (MN) et (AC) sont parallèles.
b) Calculer la distance MN.
Exercice 32
Soit (C) un cercle de centre O et de diamètre [AB] tel que
AB = 6 cm.
M est un point du cercle tel que mes (∠ABM) = 36o .
1) Faire une figure en vraie grandeur.
2) Démontrer que le triangle ABM est rectangle en M.
3) Calculer la longueur MA, arrondie au millimètre.
4) Calculer la mesure de l’angle ∠AOM.
Exercice 33
L’unité de longueur étant le millimètre.
Sient deux segments [AC] et [AB] se coupant en I.
On a :
IB = 21, ID = 27, IA = 28, IC = 36, DC = 45.
1) Faire une figure à main levée
2) Prouver que les droites (AB et (DC) sont parallèles.
3) Calculer la longueur AB.
4) Prouver que le triangle DIC est un triangle rectangle.
5) Déterminer, à un degré près, la mesure de l’angle DCI.
6) Montrer que les angles IDC et IBA ont la même mesure.
Exercice 34
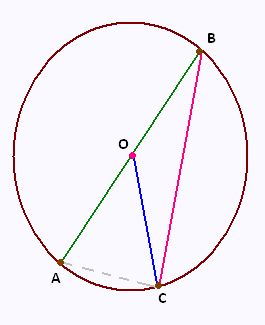
• (C) est un cercle de centre O dont le diamètre [AB]
mesure 9 cm.
• C est un point du cercle (C) tel que : mes(∠COA) = 50o.
1) Faire la figure en respectant les dimensions données.
2) Montrer que le triangle ACB est un triangle rectangle.
3) Que peut-on dire des triangles AOC et ABC ?
Calculer les angles du triangle ABC et vérifier que l'angle ∠CBA mesure 25o.
4) Calculer la longueur AC et préciser sa valeur arrondie au centième de cm.
5) On trace la droite parallèle à la droite (AC) passant par O.
Elle coupe le segment [BC] au point M.
6) Calculer la longueur OM et préciser sa valeur arrondie au dixième de cm.
Exercice 35
Soit ABC un triangle rectangle en A tel que :
AB = 6 cm et mes(∠ABC) = 40o.
1) Faire la figure en vraie grandeur.
2) Calculer AC (on donnera la valeur arrondie au mm).
3) Tracer la hauteur issue de A : elle coupe [BC] en H.
Calculer AH et en donner une valeur arrondie au mm.
Exercice 36
On considère deux droites (AC) et (BD)
se coupant en E.
L’unité de longueur est le millimètre.
On donne :
BC = 70 ; BE = 60 ; EA = 16 ;
ED = 24 ; EC = 40.
1) Faire une figure à main levée.
2) Montrer que les droites (AD) et (BC) sont parallèles.
3) Calculer la longueur AD.
Exercice 37
1) Tracer un cercle (C) de centre O et de diamètre
[AB] mesurant 8 cm.
Placer un point E sur ce cercle tel que l’angle
BAE mesure 56o.
2) Montrer que le triangle AEB est rectangle.
3) Sur le demi-cercle d’extrémités A et B, qui ne contient pas E, placer un point K.
Quelle est la valeur exacte des angles ∠EOB et ∠EKB ?
Justifier.
Exercice 38
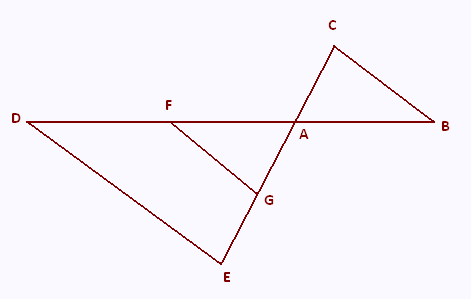
L’unité de longueur est le centimètre.
La figure ci-contre n’est pas à l’échelle.
Les points D, F, A et B sont alignés.
Les points E, G, A et C sont alignés.
Les droites (DE) et (FG) sont parallèles.
AF = 5 ; FG = 3 ; AG = 4 ; DE = 7.5 ;
AC = 3 ; AB = 3.75.
1) Démontrer que le triangle AFG est un triangle
rectangle.
2) a) Calculer AD ; en déduire FD.
b) Calculer AE ; en déduire EG.
3) Démontrer que les droites (FG) et (BC) sont parallèles.
Exercice 39
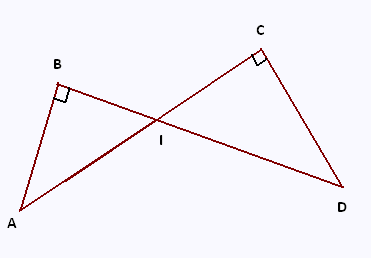
Les segments [AC] et [BD] se coupent au point I.
IC = 4 cm ; CD = 2.4 cm et AB = 4.2 cm.
Le triangle ICD est rectangle en C.
Le triangle AIB est rectangle en B.
1) Calculer la valeur exacte de la tangente de l’angle ∠CID.
2) Pourquoi les angles ∠CID et ∠AIB sont-ils égaux ?
3) Donner l’expression de la tangente de l’angle ∠AIB en fonction de IB.
4) En s’aidant des réponses aux questions précédentes,
prouver que la longueur IB en centimètres est un nombre
entier.
5) Déterminer l’arrondi au degré de l’angle ∠CID.
Exercice 40
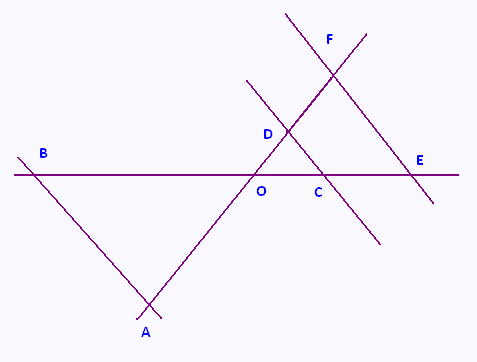
L’unité est le cm. Sur la figure ci-contre, les longueurs ne sont pas respectées. On ne demande pas de reproduire la figure.
On sait que les points B, O, C et E sont alignés dans cet ordre et que les points A, O, D, et F sont alignés dans cet ordre.
On sait également que : (AB // (DC) ; OD = 3 ; OC = 5 ; OA = 5 et DC = 4.
1) Calculer AB en justifiant ; donner la valeur exacte, puis l’arrondir au mm.
2) On sait de plus que : OF = 4.5 et OE = 7.5.
Démontrer que les droites (EF) et (DC) sont parallèles.
Exercice 41
Soit le cercle (C) de centre O et de rayon 6 cm.
[AB] est un diamètre de ce cercle.
La médiatrice du segment [AO] coupe le cercle (C) en deux points M et N.
1) Faire une figure.
2) Quelle est la nature du triangle AMB ? Justifier.
3) Quelle est la nature du triangle AON ? Justifier.
4) Montrer que l’angle mesure 30o.
|