Mathématiques
2
Mathématiques 34
Exercices de
perfectionnement
Je confirme mes acquis
© The scientific sentence. 2010
|
Mathématiques: Problèmes type brevet
Exercice 1
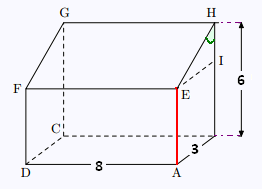
La figure ci-contre représente un gagrage. L’unité de longueur est le mètre.
• Le sol ABCD et le toit EFGH sont des rectangles.
• Le triangle HIE est rectangle en I.
• Le quadrilatère IEAB est un rectangle.
• La hauteur du sol au sommet du toit est HB.
On donne : AB = 3 ; DA = 8 ; BH = 6.
Partie 1: AE = 4
1) Calculer HI.
2) Calculer HE.
3) Calculer au degré près la mesure de l’angle IHE
Partie 2:
1) Quelle est la nature du triangle HIE? Justifier.
2) En déduire HI puis AE.
Partie 3:
1) Déterminer la valeur arrondie au cm de HI.
2) En déduire la valeur arrondie au cm de AE.
Partie 4:
La courbe ci-dessous représente la hauteur AE en fonction de la mesure de l’angle .
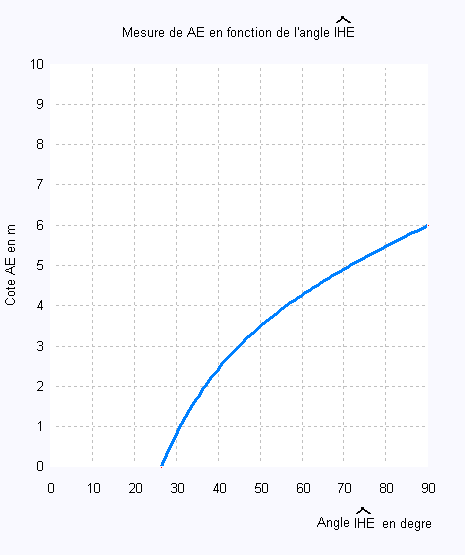
1) Placer sur la courbe ci-dessus le point P1 correspondan
à AE = 4.
Déterminer graphiquement son abscisse.
2) Placer sur la courbe ci-dessus le point P2 correspondant à
.
Déterminer graphiquement son ordonnée.
3) Placer sur la courbe ci-dessus le point P3 correspondant à
.
Déterminer graphiquement son ordonnée.
Exercice 2
Les longueurs sont exprimées en centimètres.
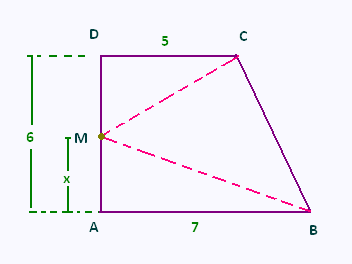
ABCD est un trapèze rectangle en A et en D tel que :
AB = 7, AD = 6, ET DC = 5.
M est un point variable du segment [AD], et on note x
la longueur du segment AM.
1) cas où x = 1
a) Faire une figure.
b) Démontrer que, dans ce cas, le triangle MDC est isocèle en D.
c) Calculer les aires des triangles AMB et MDC.
2) cas où x est quelconque
a) Donner les valeurs entre lesquelles x peut varier.
b) Calculer l'aire du triangle AMB et l’aire du triangle MDC
Voici la représentation graphique, dans le plan rapporté à un repère orthogonal, de la fonction g(x) représentant l’aire du triangle MDC en fonction de x.
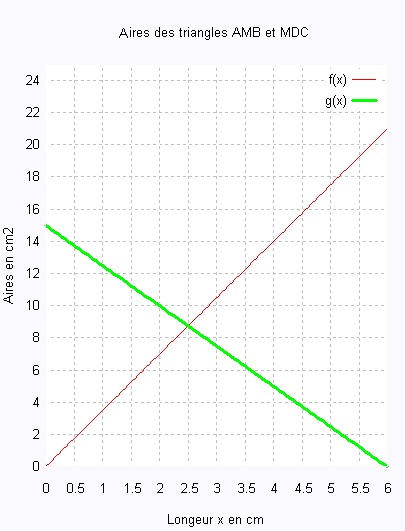
Répondre aux questions suivantes, 3. et 4., en utilisant ce graphique.
Laisser apparents les traits nécessaires.
3) a) Pour quelle valeur de x l’aire du triangle MDC est égale à 10 cm2 ?
b) Lorsque x est égal à 3 cm, quelle est l’aire du triangle MDC ?
4) a) Sur ce graphique, tracer la droite représentant la fonction f(x) représentant l’aire du triangle AMB en fonction de x.
b) Estimer graphiquement, à un millimètre près, la valeur de x pour laquelle les triangles AMB et MDC ont la même aire.
Faire apparaître les traits de construction nécessaires.
c) Montrer par le calcul que la valeur exacte de x pour laquelle les deux aires sont égales, est 5/2.
Exercice 3
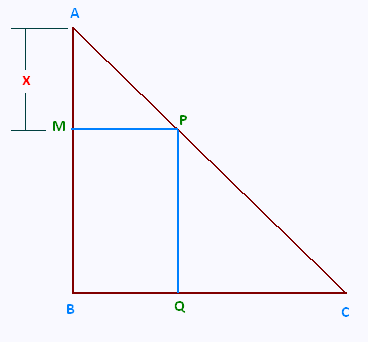
On considère un triangle ABC tel que : AC = 17.5 cm ; BC = 14 cm ; AB = 10.5 cm.
Partie 1
1) Démontrer que le triangle ABC est rectangle en B.
2) Soit M un point du segment [AB].
La parallèle à la droite (BC) passant par M coupe le segment [AC] en P.
La parallèle à la droite (AB) passant par P coupe le segment [BC] en Q.
Montrer que le quadrilatère MBQP est un rectangle.
3) Dans cette question, on suppose que le point M est situé à 5 cm du point A.
a) Calculer la longueur MP.
b) Calculer l’aire du rectangle MPQB
Partie 2:
On déplace le point P sur le segment [AB] et
on souhaite savoir quelle est la position du point
M pour laquelle l’aire du rectangle MPQB est maximale.
1) L’utilisation d’un tableur a conduit au tableau de valeurs suivant :
| Longeur AM en cm |
0 |
1 |
|
|
|
5 |
|
|
|
|
|
|
10.5 |
| Aire de MPQB en cm2 |
0 |
12.67 |
|
|
|
36.67 |
|
|
|
|
|
|
0 |
Compléter ce tableau.
2) Un logiciel a permis d’obtenir la représentation graphique suivante :
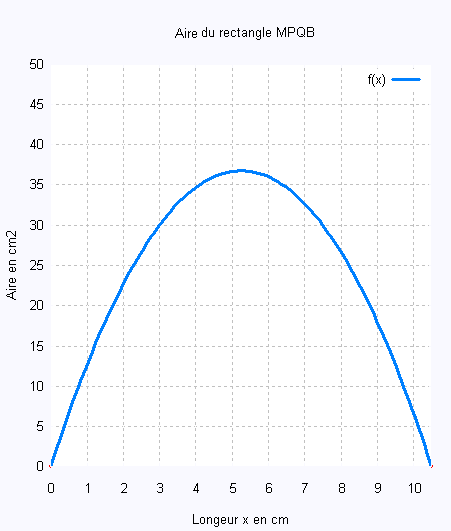
x = Longeur AM
f(x) = Aire du rectangle MPQB
À l’aide d’une lecture graphique, donner :
a) Les valeurs de AM pour lesquelles le rectangle MPQB a une aire de 30 cm2.
b) La valeur de AM pour laquelle l’aire du triangle semble maximale.
c) Un encadrement à 1 cm2 près de l’aire maximale du rectangle MPCB.
Partie: 3
1) Exprimer MB en fonction de AM.
2) Calculer le rapport MP/AM
3) Pour quelle valeur de AM le rectangle MPQB est-il
un carré ?
|
|