Mathématiques: STATISTIQUES & PROBABILITÉS

Exercice 1

On donne la série suivante :

2 ; 4 ; 8 ; 10 ; 18 ; 14 ; 17 ; 25 ; 28

a) Quelle est la médiane de cette série ?
b) Quel est le premier quartile de cette série ?
c) Quel est le troisième quartile de cette série ?

Exercice 2

Tom a lancé douze fois un dé cubique (non truqué). À chaque fois, il a obtenu 5. Il lance ce dé une 13e fois. Quelle est la probabilité d’obtenir 5 au 13e lancer ?

Exercice 3

Un sondage a été fait auprès des élèves pour connaître leur sport préféré. Les résultats sont illustrés dans le graphique ci-dessous.

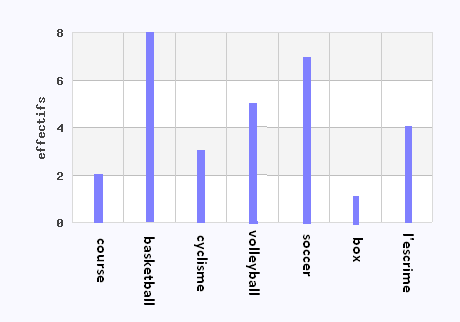
a) Quelle est la fréquence d’apparition de la réponse "velo" ?

b) Si on choisi au hasard un élève, quelle est la probabilité qu'il préfère la box?

Exercice 4

Pour un tirage au hasard, on a placé dans une urne 20 boules de même taille, les unes blanches, les autres noires.

La probabilité de tirer une boule blanche est 0.35.

Quelles sont les boules les plus nombreuses dans l’urne : les blanches ou les noires ? Expliquer.

Exercice 5

Un sondage à été réalisé auprès de 450 personnes en leur demandant le nombre de fois qu'elles sont allées au restauront durant la semaine qui vient de s’écouler.

Voici le tableau correspondant :

Nb: Nombre d'heures
Eff: Effectifs
ECC: Effectifs cumulés croissants
Freq: Fréquences
FCC: Fréquencescumulées croissantes

Nb	Eff	ECC	Freq	FCC
0	150
1	100
2	90
3
4	25
5	25
6	10
7	0

1) Compléter ce tableau.

2) a) Quel est le nombre de personnes qui sont allées une seule fois au restaurant durant la semaine qui vient de s’écouler?

b) Exprimer ce résultat en pourcentage.

3) Combien de personnes sont allées moins de 4 fois au restaurant durant la semaine qui vient de s’écouler ?

4) Combien de fois, en moyenne, les personnes interrogées ont-elles allées au restaurant durant la semaine qui vient de s’écouler?

Justifier par un calcul et arrondir le résultat à l’unité.

5) Calculer la médiane et les quartiles de cette série statistique.

6) Si on prend une personne au hasard, quelle est la probabilité qu'elle est allée 5 fois au restaurant durant la semaine qui vient de s’écouler?

7) Si on prend une personne au hasard, quelle est la probabilité qu'elle est allée au moins deux fois au restaurant durant la semaine qui vient de s’écouler?

Exercice 6

On a mélangé dans un sac 12 billes noires et 8 billes blanches.

1) Quelle est la probabilité de l’évènement « tirer une bille blanche » ?

2) Quelle est la probabilité de l’évènement « tirer une bille noire » ?

3) Quelle est la probabilité de l’évènement « tirer une bille ni blanche ni noire » ?

Exercice 7

Une urne contient cinq boules rouges dont deux sont numérotées 1 et quatre boules jaunes dont une numérotée. On extrait une boule au hasard et les boules sont indiscernables au toucher.

Quelle est la probabilité de l’évènement :

1) A : « la boule extraite est jaune » ;

2) B : « la boule extraite est numérotée » ;

3) C : « la boule extraite n’est pas jaune et n'est pas numérotée ».

Exercice 8

L’histogramme ci-dessous donne les âges de quelques personnes qui ont voté aux élections.



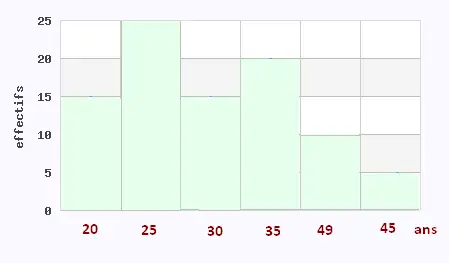
1) Combien de personnes ont voté aux élections?
2) Compléter le tableau ci-dessous. Les fréquences seront données à 0.1% près.
3) Quel est l’âge moyen des participants.

Age
Effectif
Fréquence

Exercice 9

Les résultats d’un contrôle de la vitesse des véhicules sur une autoroute ont été consignés dans le tableau ci-dessous.

Les vitesses sont regroupées en classes de 5 km/h d’amplitude.

Vitesse en km/h	75 < v ≤ 80	80 < v ≤ 85	85 < v ≤ 90	90 < v ≤ 100	105 < v ≤ 110	110 < v ≤ 120
Nombre de véhicules	22	35	55	78	14	6

1) Quel est le nombre total de véhicules contrôlés ?

2) Combien de véhicules roulent à une vitesse supérieure à la limite autorisée de 100 km/h ?

3) Quel est le pourcentage de ces automobilistes qui roulent à une vitesse supérieure à 100 km/h, se trouvant en infraction ?

4) Calculer la vitesse moyenne des véhicules dans cette autoroute. Le résultat sera arrondi à 0.1 près.

Exercice 10

Dans chacun des cas, calculer la moyenne, la médiane, les quartiles et l’étendue de la série statistique donnée.

a) Série 1: 10, 12, 17, 23, 33, 14, 20, 15, 22

b) Série 2: 10, 12 ,17, 23, 33, 14, 20, 15

c) Série 3:

valeurs	10	11	12	13	14	15	16	17	18
effectifs	2	5	12	3	6	4	11	6	8

d) Série 4:

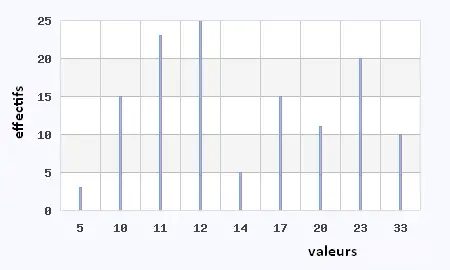
Exercice 11

Durant une compétition d’athlétisme, 7 concurrents ont couru le 100 m avec les temps suivants (en secondes) :

9.85, 9.84, 9.74, 9.58, 9.86, 9.79, 9.93

1) Classer les valeurs par ordre croissant.
2) Quelle est l’étendue de cette série ?
3) Quelle est la moyenne de cette série (arrondie au centième) ?
4) Quelle est la médiane de cette série ? Justifier.
5) Quelle est la vitesse moyenne de l’athlète classé premier,
en mètres par seconde (m.s^{- 1}), (arrondie aumillième) ?

Exercice 12

Dans une conférence on compte 24 chercheurs. Chacun d’eux vient de l’une des trois universités A, B, C et D.

• L'université A compte 8 chercheurs;
• L'université B compte 6 chercheurs;
• 45% des chercheurs appartiennent à l'université C ;
• le reste des chercheurs appartiennent à l'université D.

1) Calculer le pourcentage des chercheurs qui appartiennent à l'université A.

2) Calculer le nombre de chercheurs qui appartiennent à l'université B.

3) Représenter par un diagramme circulaire de rayon 5 cm la répartition de cette conférence entre les quatres universités A, B, C, et D.

Exercice 13

Ben sort tous ses contrôles du secondaire 3 et fait le bilan de ses notes de Mathématiques obtenues au cours de cette année.

Il a fait 22 contrôles au cours de toute l'année. Il marque une note obtenue et le nombre de contrôles où cette note a été obtenue.

Il dresse alors le tableau suivant:

note : note/100
nb contrôles: nombre de contrôles où cette note a été obtenue.

note/100	68	70	74	78	80	82	85	90	96
nb contrôles	1	1	2	1	3	2	6	4	2

1) Calculer la moyenne des notes par Ben (on donnera un résultat arrondi au dixième de point).

2) Calculer la médiane de cette série statistique.

2) Calculer le mode de cette série statistique.

2) Calculer les quartiles de cette série statistique.

Exercice 14

Dans une classe de seconde, une enquête a été menée sur « le nombre de propriétés géométriques retenues vues au collège ».

Pour celà, on a interrogé 32 élèves de la classe.

Les résultats de cette interrogation ecrite sont inscrits dans le tableau ci dessous :

nbPG: nombre de propriétés géométriques
eff : effectif

nbPG	1	12	22	25	30	40	46	50
eff	3	5	10	6	4	2	1	1

1) Calculer l’étendue de cette série statistique.

2) Déterminer la médiane de cette série statistique.

3) Déterminer, les valeurs du premier quartile et du troisième quartile de la série.

4) La proposition:

Plus des trois quarts des 32 élèves ont retenu au moins 30 propriétés géométriques vues au collège.

est-elle vraie ? Justifier la réponse.

Exercice 15

Dans un verger, on ceuille 30 mandarines comme échatillon. On les pèse une par une , sur une balance électronique, au centième près. On note la masse de chaque orange pesée. On obtient ainsi une série de masses des mandarines exprimées en grammes:

102.45, 100.00, 103.95, 105.22, 103.28, 103.28, 105.45, 105.10, 99.55, 105.22, 102.25, 99.10, 101.95, 104.25, 105.05, 100.05, 100.85, 102.00, 103.00, 101.95, 102.45, 102.25, 99.55, 102.24, 102.12, 104.35, 105.65, 103.65, 105.10,104.25.


1) Dresser le tableau des données condensées.

2) Compléter le tableau des données sous forme de calsses suivant:

classes (g)	effectif
[99.10, 100.41[
[100.41, 101.72[
[101.72, 103.03[	10
[103.03, 104.34[
[104.34, 105.65[
Total	30

3) Dresser un tableau des centres de classe.

4) Calculer la masse moyenne d'une mandarine.

5) Trouver la classe modale de la série.

6) Calculer la médiane de la série.

7) Dresser un histogramme de cette série de mandarines.

↓Réponse↑

1) Le tableau suivant représente les données condensées:

masse (g) effectif 99.10 31 99.55 32 100.00 31 100.05 31 100.85 31 101.95 32 102.00 31 102.12 31 102.24 31 102.25 32 102.45 32 103.00 31 103.28 32 103.65 31 103.95 31 104.25 32 104.35 31 105.05 31 105.10 32 105.22 32 105.45 31 105.65 31 Total 30

2) Tableau sous forme de classe: classes (g) effectif [99.10, 100.41[ 5 [100.41, 101.72[ 1 [101.72, 103.03[ 10 [103.03, 104.34[ 6 [104.34, 105.65[ 8 Total 30 3) Centres des classes: classes (g) centres [99.10, 100.41[ (99.10 + 100.41)/2 = 99.75 [100.41, 101.72[ (100.41 + 101.72)/2 = 101.06 [101.72, 103.03[ (101.72 + 103.03)/2 = 102.37 [103.03, 104.34[ (103.03 + 104.34)/2 = 103.68 [104.34, 105.65[ (104.34 + 105.65)/2 = 104.99 Total 30

4) La moyenne est éstimée à:

[5x(99.10 + 100.41)/2 + 1x(100.41 + 101.72)/2 + 10x(101.72 + 103.03)/2 + 6x(103.03 + 104.34)/2 + 8x(104.34 + 105.65)/2]/30 = 102.855 g.

5) La classe modale est
[101.72, 103.03[.

Le mode est estimé à (101.72 + 103.03)/2 = 102.375.

6) L'effectif total est n = 30.
Donc n/2 = 15. La médiane est donc la moyenne de la 15e et 16e donnée qui se trouvent dans la classe [101.72, 103.03[.

La classe médiane est donc
[101.72, 103.03[.

La médiane est estimée au milieu de la classe médiane; c'est à dire: (101.72 + 103.03)/2 = 102.375.

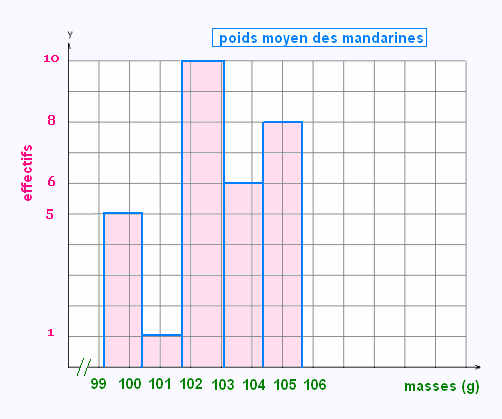
7) L’histogramme est la représentation graphique d’un tableau de données groupées en classes.

Les classes sont placées sur l’axe des abscisses.

Les effectifs sont placés sur l’axe des ordonnées.

Dans un histogramme, on mentionne le titre. Si la première classe ne commense pas par zéro, on fait une coupure d’axe (-//-).

Histogramme des masses des 30 mandarines: