Mathématiques
2
Mathématiques 34
Exercices de
perfectionnement
Je confirme mes acquis
© The scientific sentence. 2010
|
Mathématiques 45: Algèbre
Systèmes de deux équations du
premier degré à deux inconnues
Exercice 19
x et y sont deux nombres différents.
x est le premier nombre , y est le second.
On soustrait le second nombre (y) du triple du premier (x) :
3 x - y = 8 (1)
On soustrait du carré du premier nombre le double du second:
x2 - 2y = 8 (2)
de l'equation (1) on tire y = 3 x - 8 . Puis on le
porte sur
l'équation (2). On obtient:
x2 - 2(3 x - 8) = 8
x2 - 6x + 16 = 8
x2 - 6x + 8 = 0
C'est une équation du second degré . Son discriminant est:
Δ = (- 6)2 - 4 (1) (8) = 36 - 32 = 4
D'où :
x = (6 + 2)/2 = 4 → y = 3 ( 4) - 8 = 4
x = (6 - 2)/2 = 2 → y = 3 ( 2) - 8 = - 2
Les deux nombres cherchés sont donc:
4 et 4
ou
2 et - 2
Exercice 22
Méthode 1 utilisée à l'exercice 21
Parabole: d(t) = 3t2 + 2t
Droite de la tangente: g(t) = m t + n
Le point (1,5) est sur la droite de la tangente, donc:
5 = m + n ⇛ n = 5 - m
L'équation de la droite tangente est donc:
g(t) = m t + (5 - m)
Le point d'intesection de la tangente et la parabole s'obtient
en égalisant leurs équations respectives:
3t2 + 2t = m t + (5 - m)
3t2 + 2t - mt = 5 - m
3t2 + (2 - m)t + (m - 5) = 0
C'est une équation du second degré . Son discriminant est:
Δ = (2 - m)2 - 4 (3) (m - 5) =
4 - 4 m + m2 - 12 m + 60 =
m2 - 16 m + 64 =
(m - 8)2
Pour un seule solution, ce discriminant doit être égal à zéro.
d'où m = 8.
L'équation de la droite tangente devient donc:
g(t) = 8 t - 3
La pente , qui est égale à 8, de la droite tangente
à la parabole au point A(1,5) est la vitesse, en m/s, de la bille
en ce point.
Méthode 2
Taux de variation de la fonction d(t) au point A(1,5):
v(t) = Δd(t)/Δt = [(3t2 + 2t) - 5 ]/(t - 1),
qu'il faut évaluer à t = 1.
Au numérateur, nous avons:
3t2 + 2t - 5
C'est une fonction quadratique qu'il faut factoriser.
Pour son équation du second degré, le discriminant est:
Δ = 22 - 4 (3) - 5) = 64
Les solutions sont donc:
t = (- 2 - 8)/6 = - 5/3 et
t = (- 2 + 8)/6 = 1
Donc:
3t2 + 2t - 5 = 3(t - 1 )(t + 5/3)
L'expression de v(t) devient:
v(t) = 3(t - 1 )(t + 5/3) /(t - 1)
Qui se simplifie et devient:
v(t) = 3 (t + 5/3) = 3t + 5
Pour t = 1 : v(1) = 8 m/s
Exercice 18
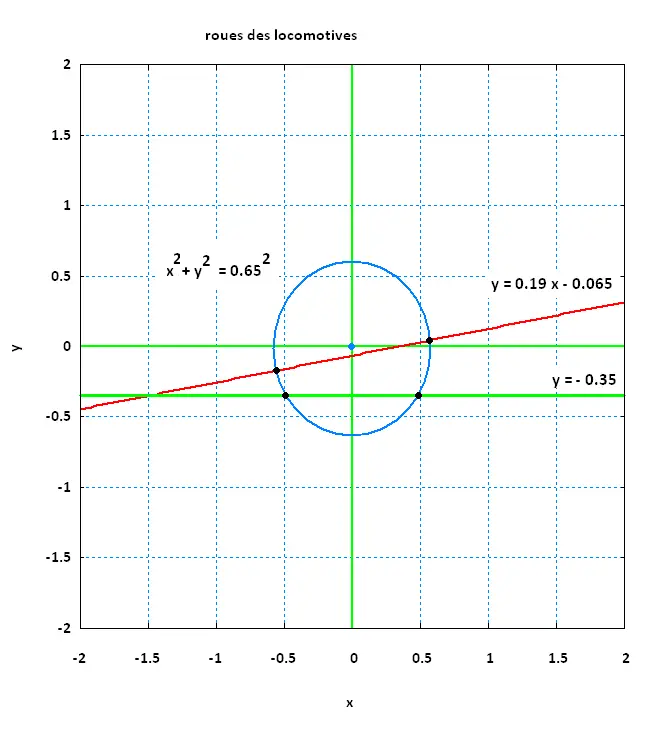
A(- 1.5, - 0.35)
B(1.5, 0.22)
C(1.8, - 0.35)
a)
• Droite (AB):
- 0.35 = - 1.5 a + b
0.22 = 1.5 a + b
On additionne selon la méthode de réduction:
2 b = - 0.13 ⇒ b = - 0.065
a = (0.22 + 0.065)/1.5 = 0.19
(AB) y = 0.19 x - 0.065
• Droite (AC) :
- 0.35 = - 1.5 a + b
- 0.35 = 1.8 a + b
On soustrait selon la méthode de réduction:
0 = - 3.3 a ⇒ a = 0 . Donc b = - 0.35
(AC): y = - 0.35
b)
1.
(Cercle): x2 + y2 = 0.4225
(AB): y = 0.19 x - 0.065
x2 + (0.19 x) 2 - 2 x 0.19 x 0.065 x + 0.0652 = 0.4225
x2 + (0.19 x) 2 - 2 x 0.19 x 0.065 x + 0.0652 - 0.4225 = 0
1.036 x2 - 0.0247 x - 0.4182 = 0
Δ = 0.02472 - 4(1.036)(- 0.4182) = 1.73
√Δ = 1.32
x = (0.0247 + 1.32)/ 2 x 1.036 = 0.65
x = (0.0247 - 1.32)/ 2 x 1.036 = - 0.62
y = 0.19 (0.65 ) - 0.065 = 0.06
y = 0.19 (-0.62 ) - 0.065 = - 0.183
Points d'intersection:
(0.65,0.06) et (- 0.62,- 0.183)
2.
(Cercle): x2 + y2 = 0.652
(AB) y = - 0.35
(Cercle): x2 + (- 0.35 )2 = 0.652
x2 = 0.652 - (- 0.35 )2 = 0.3
x = 0.55
x = - 0.55
Points d'intersection:
(0.55, - 0.35) et (- 0.55- 0.35)
Exercice 20
La moyenne arithmétique de deux nombres a et b est ma = (a + b)/2.
Leur moyenne proportionnelle est mp = √ab, et leur moyenne
harmonique est mh = 2ab/(a + b)
a) Trouver deux nombres a et b avec ma = 4, et mp = 3.
b) Trouver deux nombres a et b avec ma = 4, et mh = 3

Exercice 16
La différence de deux nombres est égale à 3. La différence de
leur carré vaut 6. Calculer la différence des cubes de ces nombres.
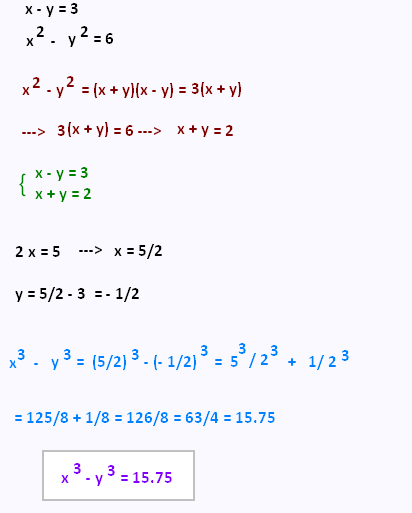
Exercice 17
Trouver le nombre de points d'intersection entre une
parabole et droite selon la valeur du paramètre k.

|
|