Mathématiques: Géométrie:
DROITES REMARQUABLES
Exercice 1
1) Retrouver la définition de la bissectrice d'un angle.
2) Construire à la règle et au compas les trois bissectrices d’un
triangle PQR tel que : PQ = 10 cm, QR = 7 cm et PR = 4 cm.
3) Rappeler la propriété des bissecrices d’un triangle.
4) Tracer le cercle inscrit au triangle PQR.
Exercice 2
1) Construire un triangle ABC tel que AB = 11 cm, BC = 6 cm et AC = 9 cm.
2) Tracer en bleu la médiane issue de A.
3) Tracer en vert la médiatrice du segment [BC].
4) Tracer en rouge la hauteur issue de C.
Exercice 3
1) Retrouver les deux définitions de la médiatrice d’un segment [AB].
2) Construire à la règle et au compas les trois médiatrices d’un
triangle PQR tel que : PQ = 10cm, QR = 7cm et PR = 4cm.
3) Rappeler la propriété des médiatrices d’un triangle.
4) Tracer le cercle circonscrit au triangle PQR.
Exercice 4
1) Retrouver la définition de la médiane d'un côté
d'un triangle.
2) Construire à la règle et au compas les trois médianes
d’un triangle PQR tel que : PQ = 10 cm, QR = 7 cm et PR = 4 cm.
3) Rappeler la propriété des médianes d’un triangle.
4) Rappeler la propriété du centre de gravité d'un triangle.
Exercice 5
1) Retrouver la définition de la hauteur dans un
triangle .
2) Construire à la règle et au compas les trois hauteurs d’un
triangle PQR tel que : PQ = 10cm, QR = 7cm et PR = 4cm.
3) Rappeler la propriété des hauteurs d’un triangle.
Exercice 6
Construire le triangle ABC et son cercle inscrit tel
que AB = 13 cm, BC = 9 cm et AC = 8 cm.
On fera très attention à la propreté de la figure
(couleurs, codage, précision).
Exercice 7
Tracer un segment [AB] de longueur 6 cm de milieu M.
Tracer le cercle de centre B qui passe par M.
Construire la tangente (d) à ce cercle en M.
Que représente (d) pour le segment [AB] ? Justifier.
Exercice 8
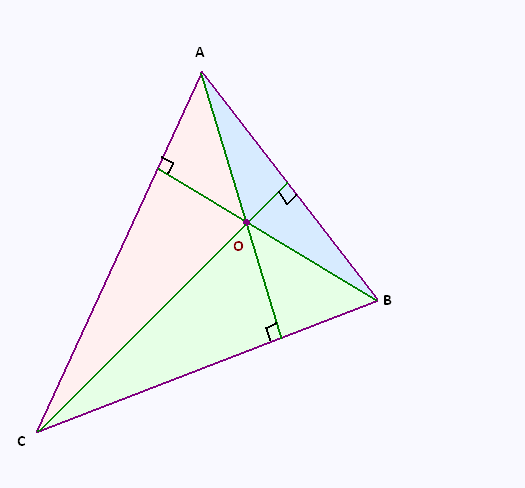
O est l’orthocentre du triangle ABC.
Quel est l’orthocentre des triangles :
– AOB ?
– BOC ?
– AOC ?
Exercice 9
Construire un losange ABCD tel que AC = 8 cm et BD = 5 cm.
La perpendiculaire à la droite (AD) passant par
le point C est sécante au point E avec la droite (BD).
1) En considérant le triangle ACD, que peut-on dire des
droites
(BD) et (CE) ? Justi?er votre réponse.
2) Que représente alors le point E ?
3) Les droites (AE) et (CD) sont-elles
perpendiculaires ? Justifier votre réponse.
Exercice 10
1) Construire un triangle ABC tel que AB = 7 cm, AC = 5 cm et
BC = 8 cm.
2) Rappeler les définitions de la médiatrice d’un segment [AB].
3) Tracer le cercle circonscrit de ce triangle. On appellera O son centre.
4) I est le milieu de [OB] et J celui de [OC]. Calculer IJ.
Exercice 11
1) Construire un triangle ABC tel que AB = 6 cm, BC = 4 cm et AC = 8 cm.
2) Placer le point P tel que ABCP soit un parallélogramme.
3) Dans le triangle ABC, tracer les hauteurs issues de A et de B.
4) On appelle H le point d’intersection de ces deux hauteurs.
Que peut-on dire du point H ?
5) Montrer que (AB) est perpendiculaire à (CH).
6) Quelle est la nature du triangle CPH ? Justifier.
Exercice 12
Un triangle équilatéral ABC a pour hauteur 6 cm.
1) Donner les définitions du centre du cercle inscrit et du centre du cercle circonscrit dans le cas général.
2) Que peut-on dire dans ce cas particulier du centre du cercle inscrit et du centre du cercle circonscrit ?
3) Donner la mesure du rayon du cercle inscrit et la mesure du rayon du cercle circonscrit.
Exercice 13
Soit un cercle de centre O et de diamètre [AB] mesurant 8 cm.
La médiatrice du segment [AO] coupe le cercle en deux points C et D.
1) Faire une figure en vraie grandeur en traçant les
côtés du triangle ABC.
2) Que peut-on dire du triangle ABC ? Justifier.
3) Que représente la droite (CD) dans le triangle ABC ?
4) Que représente le segment [OC] dans le triangle ABC ?
|