Mathématiques: Algèbre et Géométrie
EQUATIONS
Exercice 1
Résoudre l’équation:
2(x + 2) = 4(3x - 4).
Exercice 2
Une mère de 43 ans a quatre enfants âgés de 10, 12, 14, et 16 ans.
Dans combien d’années le double de l’âge de la mère sera-t-il égal à la somme
des âges de ses enfants ?
Exercice 3
Une mère de 40 ans a deux enfants âgés de 12 et 14 ans.
Dans combien d’années l’âge de la mère sera-t-il égal à
la somme des âges de ses enfants ?
Exercice 4
Après les taxes de 15%, un livre coûte 143.55 $. Quel
était son prix sans taxes ?
Exercice 5
Résoudre les équations :
• 3x - 2(x - 3) = 6 + 4(1 - 2x).
• 2(5 - x/4) = 2/3 - 2(1/3 - x/2)
Exercice 6
Deux nombres ont pour somme 30.
L’un est égal aux sept huitième de l’autre.
Quels sont ces deux nombres ?
Exercice 7
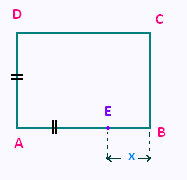
ABCD est un rectangle; l’unité de longueur est le
centimètre.
On a : AE = AD = 5 et EB = x.
1) Calculer le périmètre de ABCD en fonction de x.
2) Trouver x pour que le périmètre de ABCD soit
égal à 30.
Exercice 8
Résoudre l’équation :
5(2x - 3) - 7(-x - 4) = -2x + 5 - 3(2x - 4).
Exercice 9
On veut résoudre l’équation : (x - 6)(2x - 8) = (2x - 1)(x + 5).
1) Développer et réduire chaque membre de cette équation.
2) Résoudre l’équation ainsi obtenue.
Exercice 10
Résoudre les équations suivantes :
a) 2x + 3 = -7
b) 3x + 1 = x - 3
c) 4 - 12x = 10 - 14x
d) -2x + 8 = x - 13.
Exercice 11
Trois amis se partagent les frais de location d'un
camion pour leur déménagement qui s'élèvent à
760$.
– Max paye le double de Jim moins la somme de 240 $.
– Daria paye le triple de Max moins la somme de 460 $.
On veut savoir si le partage est équitable.
1) On appellera x la somme payée par Jim.
a) Exprimer en fonction de x la somme payée par Max.
b) Exprimer en fonction de x la somme payée par Daria.
2) Résoudre l’équation :
x + (2x - 240) + (3x - 460) = 760.
3) Quelle somme a payée Marc ?
Quelle somme a payée Max?
Quelle somme a payée Daria ?
4) Le partage est-il équitable ?
Exercice 12
Résoudre l’équation : 5(x - 8) = 9 - 2x.
Exercice 13
Afin de découvrir des attractions et surtout les dauphins,
au parc aquatique Marineland, à Niagara Falls , en
Ontario (5 minutes des célèbres Chutes), on se fixe
sur le choix suivant:
"FIVE GREAT ATTRACTIONS AT ONE LOW PRICE!
$... /ADULT & ... CHILD! "
La recette d'un jour de ce parc d'attractions est de 11 175 $ .
Dans le public, on a compté 200 adultes et 300 enfants.
le tarif enfant coûte 6 $ de moins que celui d’un adulte.
Quels étaient les tarifs d’entrée ?
Exercice 14
Déterminer les valeurs de x qui vérifient l’inégalité :
4x - (x + 1) ≥ 12x.
Exercice 15
Résoudre l’équation :
(3/4)x - 5 = x + 3.
Exercice 16
Aujourd’hui, Alexandre a 8 ans et Roxane a 20 ans.
Dans combien d’années l’âge de Roxane sera-t-il le double
de celui d'Alexandre ?
On détaillera la démarche utilisée.
Exercice 17
Résoudre l’équation 2(3x - 5) - 4(x + 3) = 2(3 + 2x).
Exercice 18
Résoudre les équations suivantes :
a) 3x + 2 = x - 5
b) 7x - 5 = 9x + 1
c) 4 - 12x = -7 - 14x
d) - 4x + 8 = x - 14.
Exercice 19
Résoudre les équations suivantes :
a) x/2 + 3 = 5/4 - (2/3) x
b) (1/2)y - 3/4 = y/5 - y/5 + 1/3
c) (5/9) x + 2 = 11/9
d) (4/5)z + 1 = 5/3 - (2/3)z
Exercice 20
Résoudre les équations suivantes :
a) (3/2)x - 4 = x + 4
b) 2x - 2/3 = x/5 + 3
c) (3x - 3)/5 = (8x - 3)/6
d) (2/5)x + 2/3 = 1/6 - x/2
Exercice 21
Résoudre les équations suivantes :
a) 5(x - 6) = 30
b) 3 + (1 - y) = 20
c) -5(2x + 3) = -25
d) 1 - 5(2x + 4) = - 23
Exercice 21
Résoudre les équations suivantes :
a) 2(x + 3) = 3(x + 2)
b) 3(5 - 2y) = 2(y - 1)
c) 3 + 2(y - 1) = 3y + 6
d) 5x - 2(3x + 1) = 2(x - 7).
Exercice 22
Résoudre les équations suivantes :
a) 4x/3 - 2/3 = x/5 + 4/5
b) 2/7 - (1/6)x = (1/3)x + 1/12
c) 7/10 - (1/5)x = 1/20
d) x/8 - 1/8 = (-1/4) - x/2
Exercice 23
Déterminer trois nombres entiers consécutifs dont la
somme est égale à 369.
Exercice 24
Existe-t-il trois nombres entiers consécutifs dont la somme
est 123 ?
Justi?er votre réponse.
Exercice 25
Déterminer quatre nombres entiers consécutifs dont la somme est
égale à 106.
Exercice 26
Déterminer trois nombres relatifs dont la somme est 10 et tels que :
• le deuxième soit la somme du premier et de 5,
• le troisième soit le triple du deuxième.
Exercice 27
On a déjà lu 52 pages d'un livre.
Si, de plus, on lit un tiers du livre, on aurait lu
sa moitié.
Quel est le nombre total des pages du livre?
Exercice 28
Pour faire un café au lait, on dose de la manière suivante :
trois volumes de lait pour un volume de café noir.
Quelles seront, en centilitres, le volume de café et le volume
de lait nécessaire pour obtenir un tasse de 35 cl de cet
café au lait.
Exercice 29
Trouver, par essais, trois solutions de l’équation :
x3 - 2 x2 - x + 2 = 0.
Exercice 30
Un rectangle est deux fois plus long que large.
Si augmente la largeur de 8 mètres et la longueur de 2 mètres,
on obtient un carré.
Quelles sont les dimensions de ce rectangle ?
Exercice 31
L'Inde compte actuellement 1 274 800 000 habitants.
Le taux de croissance de sa population est de 1,76%
Quelle était sa population il ya un an?
Exercice 32
Résoudre les équations suivantes :
a) 5x = 20
b) y + 107 = 37
c) 5x + 4 = 29
d) 7x - 12 = 2
e) 2x + 15 = 6x + 3
f) 8x - 1 = 5x - 157
Exercice 33
Marie-Claire achète un livre de Maths, un romain et un livre de bricolage.
Le prix du livre de Maths est le double de celui du prix du roman.
Le prix du livre de bricolage est le triple de celui du roman.
Elle paye 290.00 paye et on lui rend 8.90 $.
Quel est le prix de chaque ouvrage?
Exercice 34
On achète des livres de Maths et de Physique.
La prix total payé pour ... livres ensemble est ... $.
Le prix d'un livre de Maths est 100 $, celui de
physiqe est ... $.
Quel est le nombre de livre de chaque matière?
1) Retrouver les nombres manquants conformément aux
démarches suivantes:
Soit x le nombre de livres de Maths.
(10 - x) est le nombre de livres de Physique.
D’où l’équation : 100x + 80(10 - x) = 1440.
2) Répondre à la question posée dans l’énoncé.
Exercice 35
Sachant que x < 6, que peut-on en déduire pour :
1) x + 9 ?
2) x - 13 ?
3) 0.5x ?
4) - 2x ?
5) - (4/3)x ?
|