Mathématiques:
PROPORTIONNALITÉ
Exercice 1
Ce tableau de valeurs est-il un tableau de
proportionnalité ?
Exercice 2
Ce tableau de valeurs est-il un tableau de
proportionnalité ?
Exercice 3
Dans ce tableau de proportionnalité, quelle
"formule" permet de calculer le nombre
manquant x ?
x = 15 x (5/3)
x = (15/5) x 3
x = 15 x (3/5)
x = (15/3) x 5
Exercice 4
Tom est agé de 15 ans, et il mesure 1 m 55.
Si son âge et sa taille étaient proportionnels,
combien mesurerait-il obligatoirement à 33 ans ?
Exercice 5
Le plan d'un terrain est à l’échelle 1/1000.
.
Cela signifie que :
• Les longueurs sur le plan sont 1000 fois plus grandes que les distances réelles
• Les longueurs sur le plan sont 1000 fois plus petites que les distances réelles
• Pour passer des distances réelles aux longueurs sur le plan, on multiplie par 1000
• Pour passer des distances réelles aux longueurs sur le plan, on divise par 1000
• Pour passer des longueurs sur le plan aux distances réelles, on multiplie par 1000
• Pour passer des longueurs sur le plan aux distances réelles, on divise par 1000
Exercice 6
Pour chacun de ces énoncés, répondre à la question par oui ou par non. Justifier.
1- 30 m de fil électrique pèsent 4.0 kg.
La longueur du fil et sa masse sont-elles des grandeurs proportionnelles ?
2- 5 kg d'oranges coûtent 4.50 $.
La quantité achetée et le prix à payer sont-ils des grandeurs proportionnelles ?
3- Le côté d’un triangle équilatéral et son périmètre sont-ils des grandeurs proportionnelles ?
4- La hauteur h d'un parallélépipède rectangle et le volume du solide sont-ils des grandeurs proportionnelles ?
5- Un piéton marche à la vitesse de 4 km/h.
La durée de son trajet et la distance parcourue sont-elles des grandeurs proportionnelles ?
6- L’arête d’un cube et son volume sont-ils des grandeurs proportionnelles ?
7- Le périmètre d'un CD et son rayon R sont-ils des grandeurs
proportionnelles ?
Exercice 7
Chacun des tableaux suivants correspond-il à une situation de proportionnalité ? Si c’est le cas, quel
est le coefficient de proportionnalité ?
Ne pas utiliser de calculatrice .
| 2 |
4 |
6 |
8 |
10 |
| 22 |
44 |
55 |
88 |
110 |
Exercice 8
Un motocycliste a parcouru 75 km en consommant 2 L de carburant.
1- Expliquer pourquoi la quantité de carburant et la distance parcourue sont des grandeurs proportionnelles.
2- Compléter les tableaux suivants (sans calculatrice) :
| Distance
(en km) |
75 |
5 |
15 |
120 |
150 |
| Consommation
(en L) |
2 |
... |
... |
... |
... |
| Distance
(en km) |
75 |
... |
... |
... |
... |
| Consommation
(en L) |
2 |
4 |
3 |
3 |
1.5 |
Exercice 9
En 2 h, un automobiliste a parcouru 170 km. La quantité de distance parcourue et la durée de voyage sont proportionnelles.
On appelle x la durée nécessaire en h pour parcourir 2.5 km.
Construire un tableau correspondant aux données de cet exercice, puis calculer x en heures minutes.
Exercice 10
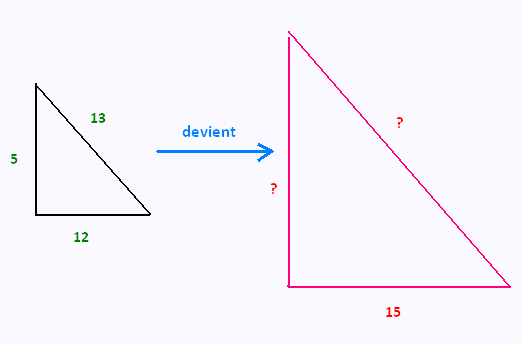
On agrandit un triangle rectangle:
1 - Calculer l'échelle de l'agrandissement.
2 - Calculer les mesures inconnues.
3 - Calculer le périmètre et l'aire des triangles.
4 - Quelle remarque peux-t-on faire sur l’évolution du périmètre et l’évolution de l’aire ?
Calculer pour
cela le rapport entre ces grandeurs avant et après agrandissement.
Exercice 11
Voici une série de questions.
Pour chacune, dire si elle relève d’une situation de proportionnalité.
1- Sur une carte, une route de 10 km est représentée par un segment de 25 cm.
Quelle longueur sur la carte représentera une route de 35 km ?
2- Sébastien parcourt, en vélo, 20 km en 1 h et demie.
Combien de temps lui faut-il pour parcourir 15 km ?
Traduis cette durée en minutes.
3- Daria a 20 ans, et son petit frère 14 ans.
Quand Daria aura 60 ans, quel âge aura son petit frère ?
5- Avec 120.00 $ on peux acheter 6 romans.
Combien de romans peux-t-on acheter avec 30 $ ? Et avec
360.00$ ?
Combien coûtent 12 romans Et 22 romans ?
Exercice 12
Un triangle ABC est tel que : AB = 7 cm BC = 5 cm AC = 6 cm.
Tracer un agrandissement de ce triangle, sachant que le côté [BC] devra mesurer 9 cm.
Exercice 13
1- Voici un tableau de proportionnalité :
a) Quels rapports sont égaux ?
b) Prouver que l’on a : 5 x = 4 x 20.
c) Quel calcul permet d’obtenir le nombre x ?
2- Voici un autre tableau de proportionnalité :
Prouver que l’on a : 28 y = 7 x 12.
Quel calcul permet d’obtenir le nombre y ?
Exercice 14
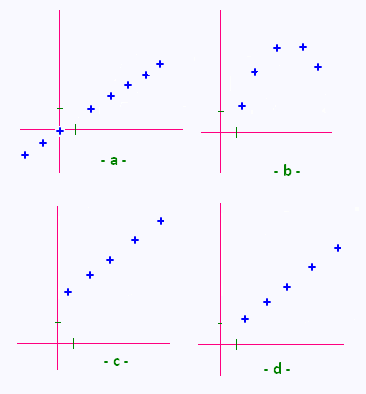
Parmi ces 4 ensembles de points, lesquels sont représentatifs d’une situation de proportionnalité ?
Justifier la réponse.
Exercice 15
La voiture de Jim consomme 9.5 L de carburant pour
100 km.
La quantité de carburant et la distance parcourue
sont-elles des grandeurs proportionnelles ?
Justifier.
Exercice 16
Dand une joaillerie, on vend des bagues en or 9 carats, 14 carats, et
18 carats.
Quelle quantité d'or pur trouve-t-on dans une bague
d'or de 18 carats et qui pèse 100 g?
Pour l'or, le carat est la purete du metal 9,14.18 ou 24.
Pour les pierres précieuses, le carat est l'unité de mesure
de la masse de la pierre. 1 carat = 0.2. g
L'or pur de 24 carats étant trop mou pour la fabrication d'un bijou.
Pour le durcir, il est donc allié avec un mélange d'autres métaux comme
l'argent, le cuivre, le nickel ou le zinc.
• L’or 18 carats signifie que dans 24 g d’alliage il y a 18 g,
soit 75.01% d'or pur. Il est également appelé or 750/1000ème.
• L’or 14 carats signifie que dans 24 g d’alliage il y a 14 g,
soit 58.5% d'or pur. Il est également appelé or 585/1000ème.
• L’or 9 carats signifie que dans 24 g d’alliage il y a
9 g, soit 37.5% d'or pur. Il est également appelé or 375/1000ème.
Exercice 17
1 m3 d'eau de mer contient 0.004 mg d’or.
Le volume total d'eau de mer sur la Terre est estmé à
1.4 milliards de Km3.
Quelle est la masse totale d’or (en tonnes) que contient
toute l'eau de mer ?
|