Mathématiques:
PYRAMIDES & CÔNES
Exercice 1
Compléter les pointillés suivants :
1 -
65 L = ... dL
5.8 daL = ... mL
.0073 kL = 73 ... .
4500 cL = 0.45 ...
2 -
1 L = ... dm3
1 dL = ... dm3 = ... cm3 = ... dam3
58 L = ... cm3 = 0.058 ... .
Exercice 2
Calculer le volume d’une pyramide dont la base est un carré de côté 12 cm et la hauteur mesure 15.5 cm.
Exercice 3
Calculer le volume d’un cône de révolution dont la hauteur est 30 cm et de rayon 6 cm
Exercice 4
Calculer le volume d’un cône de révolution dont la génératrice est de 50 cm et de rayon 30 cm.
Exercice 5
Une pyramide a pour base un triangle ABC tel que BC = 6 cm, [AH] est la hauteur de ce triangle issue de A et relative de [BC] et AH = 4 cm.
a) Tracer une figure à main levée.
b) Exprimer la hauteur h de la pyramide en fonction de son volume V.
c) Si son volume est égal à 40 cm3, quelle est sa hauteur ?
d) Si son volume est égal à 120/3 cm3, quelle est sa hauteur ?
Exercice 6
Un cône a un volume de 10 π cm3.
a) Exprime son rayon au carré R2
en fonction de son volume V et de sa hauteur h.
b) Si sa hauteur est égale à 5 cm, calculer son rayon.
c) Exprimer sa hauteur en fonction de son rayon et de son volume.
d) Si son rayon est égal à 7 cm, calculer sa hauteur.
Donner la valeur exacte puis la valeur arrondie au mm près.
Exercice 7
1- Calculer la hauteur d’un cylindre de volume V = 0.144 π L et de rayon de base R = 4 cm.
2- Calculer l’aire latérale de ce même cylindre, en cm2, en donnant la valeur exacte, puis la valeur arrondie au
centième près.
Exercice 8
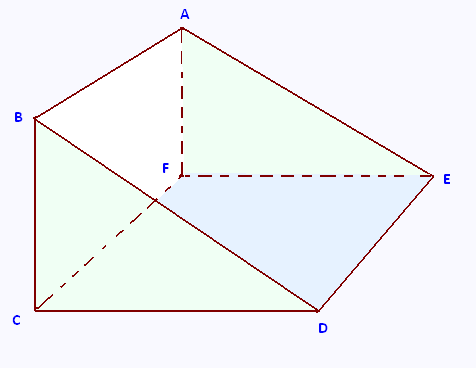
On considère le prisme ci-contre:
On a :
• FC = 5 cm
• BC = 6 cm
• Le volume V de ce prisme est tel que :
V = 210 cm3.
1- Calculer l’aire de chaque base.
2- Calculer CD.
3- Construire un patron de ce prisme à main levée en indiquant les longueurs de chaque côté.
Exercice 9
Une piscine a la forme d’un pavé droit. Sa largeur est 10 m et sa hauteur 2 m. Elle peut contenir au maximum 320 m3.
d’eau.
1- Quelle est sa longueur ?
2- Il y a une hauteur d’eau de 1.6 m dans la piscine.
Calculer le volume d’eau en m3 puis convertis-le
en litres.
3- Calculer la hauteur d’eau en m sachant que le volume d’eau est de 256 000 L.
Exercice 10
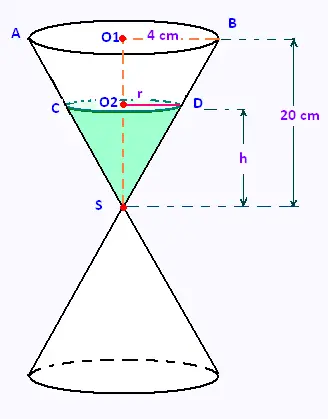
1-
Dans un sablier, on a mis 12 cm de hauteur de sable.
Le sable s’écoule au débit de 120 mm3
par seconde.
On cherche à savoir combien de temps mettra le sable
pour s’écouler totalement.
a) En utilisant la propriété de Thalès, calculer la valeur du
rayon r en cm puis en mm pour une hauteur de sable
h = 12cm.
b) Calculer le volume du sable en fonction de π en cm3 puis en mm3.
Donner ensuite la valeur arrondie au mm3 près.
c) Combien de temps mettra le sable pour s’écouler
totalement.
Arrondir à la seconde près.
2- :
Quelle hauteur de sable devra-t-on mettre pour que le
temps mis pour qu’il s’écoule en totalité soit de quatre minutes?.
a) Démontrer que le volume de sable s’écoulant pendant 4 minutes est de 28 800 mm³.
Soit h la hauteur de sable nécessaire et r le rayon du disque correspondant à cette hauteur, en cm.
b) En utilisant la propriété de Thalès dans le triangle SO1B, exprime r en fonction de h.
c) Exprime le volume Vh en fonction de la hauteur h, de r et de π.
d) En utilisant les deux questions précédentes, exprime Vh en fonction de h et de π.
|