Mathématiques: Géométrie
PROPRIÉTÉ DE PHYTAGORE ET SA RECIPROQUE
Exercice 1
Soit ABCD un losange de centre O et de côté 5.5 cm
tel que AC = 8.4 cm.
1) Rappeler les propriétés d’un losange:
a) Propriétés des côtés,
b) Propriétés des diagonales.
2) Faire une figure en vraie grandeur.
3) Calculer OB.
Exercice 2
Soit ABC un triangle tel que AB = 48 mm, AC = 80 mm et BC = 6.4 cm.
M est le milieu du segment [AC].
1) Le triangle ABC est-il rectangle? Justifier.
2) Calculer BM.
3) Donner la définition de la tangente au cercle
circonscrit au triangle ABC au point B.
Exercice 3
L’unité de longueur est le centimètre.
Soit ABC un triangle rectangle en A tel que AB = 10 et BC = 12.
1) Quel est le nom de l’hypoténuse de ce triangle ?
2) Calculer la longueur AC en détaillant la démarche.
3) Tracer le triangle ABC.
Exercice 4
Soit ABC un triangle tel que :
AB = 104 mm, AC = 96 mm et BC = 4 cm.
1) Faire une figure qui sera complétée au fur et à mesure.
2) Démontrer que ABC est un triangle rectangle.
3) Soit D le point du segment [AB] tel que AD = 78 mm.
Le cercle (C) de diamètre [AD] coupe le segment[AC] en E.
Préciser la nature du triangle AED. Justifier la réponse.
4) Démontrer que les droites (BC) et (DE) sont parallèles.
5) Calculer AE.
Exercice 5
Soit ABCD un carré de côté 76 mm.
1) Faire une figure à main levée.
2) Calculer la longueur de sa diagonale à 1 mm près.
Exercice 6
ABCD est un losange de centre O, tel que BD = 6.4 cm et AB = 4 cm.
1) Faire une figure en vraie grandeur.
2) Calculer la longueur de la diagonale [AC].
Justifier.
Exercice 7
Soit ABC un triangle rectangle en C tel que AB = 7 cm et BC = 5 cm.
1) Faire une figure en vraie grandeur.
2) Calculer AC au dixième près.
Exercice 8
Soit le triangle ABC tel que
AB = 6 cm, AC = 15.6 cm et BC = 14.4 cm.
1) Faire une figure.
2) Le triangle ABC est-il rectangle ?
On expliquera les étapes de la démarche.
Exercice 9
Soit ABCun triangle rectangle en B tel que AB = 9 cm et BC = 6 cm.
1) Faire une figure en vraie grandeur.
2) Calculer AC au dixième près.
Exercice 10
Soit le triangle ABC tel que AB = 7.7 cm, AC = 5.4 cm et BC = 5.5 cm.
1) Faire une figure.
2) Le triangle ABC est-il rectangle ?
Exercice 11
ABC est un triangle tel que AB = 4.5 cm ; AC = 2.7 cm ; BC = 3.6 cm.
Démontrer que le triangle ABC est un triangle rectangle.
Exercice 12
1) Rappeler les propriétés d’un rectangle
a) Propriétés des côtés
b) Propriétés des diagonales.
2) Tracer un cercle de centre I et de diamètre AB = 12 cm.
3) Terminer la construction d’un rectangle ACBD tel que BC = 5 cm.
4) Calculer AC.
Exercice 13
ABC un triangle et H le pied de la hauteur issue de B.
H est situé sur le segment [AC] tel que AH = 2 cm.
On donne AC = 13 cm et BH = 5 cm.
1) Faire une figure.
2) Calculer AB puis sa valeur approchée au dixième.
3) Calculer BC puis sa valeur approchée au dixième.
4) Le triangle ABC est-il rectangle ?
Exercice 14
Soit ABC un triangle isocèle de sommet principal C.
On donne AB = 10.8 cm et AC = 9 cm.
Soit M le milieu du segment [AB].
1) Faire une figure.
2) Pourquoi peut-on affirmer que le triangle AIC est rectangle en M ?
3) Calculer CM.
4) En déduire l’aire du triangle ABC.
Exercice 15
ABCD est un losange de centre O tel que AC = 12 cm et BD = 8 cm.
1) Faire un schéma à main levée.
2) Faire une figure en vraie grandeur.
3) Calculer AB.
4) En déduire le périmètre du losange ABCD.
Exercice 16
ABC est un triangle rectangle en B tel que AB = 8 cm et AC = 12 cm.
1) Faire une figure en vraie grandeur
.
2) Calculer BC. On arrondira la valeur au mm.
Exercice 17
Soit un cerlce (C) de diamètre [AB] mesurant 12 cm.
Un autre cercle de centre A et de rayon 6 cm coupe (C)
en deux points C et D.
1) Faire une figure en vraie grandeur.
2) Que peut-on dire du triangle ABC ? Justifier.
3) Calculer BC.
Exercice 18
Questions à choix multiples: Pour a) et b) ensemble,
deux réponses sont vraies.
a) La Propriété de Pythagore sert à :
- calculer une longueur inconnue dans un triangle.
- calculer l'aire d'un triangle rectangle.
- calculer une longueur inconnue dans un triangle rectangle.
b) Sa réciproque sert à :
- calculer la mesure des angles d'un triangle.
- démontrer qu'un triangle est rectangle.
- calculer une longueur inconnue dans un triangle rectangle.
Exercice 18
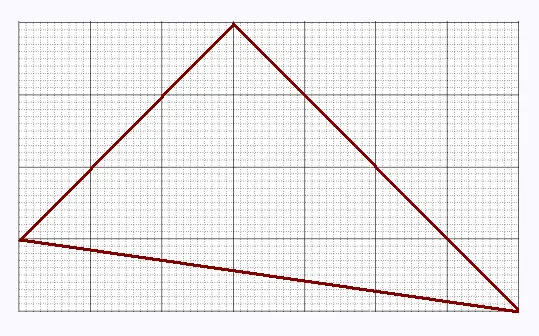
Dans cette figure, un carreau représente 10 mm x 10 mm.
a) Nommer les sommets de ce triangle,
b) Calculer les mesures de ses côtés,
c) Calculer son aire de deux façons différentes.
|