Mathématiques: Géométrie
PROPRIÉTÉ DE PHYTAGORE ET SA RECIPROQUE

Exercice 1

ABC est un triangle tel que AB = 8 cm, BC = 6 cm et AC = 10 cm.

M est le point du segment [AB] tel que MB = 5 cm. La parallèle à la droite (BC) passant par M coupe le segment [AC] en N.

1) Faire une figure.
2) Montrer que ABC est un triangle rectangle.
3) Calculer AN et MN.

Exercice 2

ABCD est un parallélogramme tel que :
AB = 8 cm ; AD = 12 cm et BD = 10 cm.

1) a) Faire une figure à main levée sur laquelle on écrira les longueurs.
b) Faire la figure en vraie grandeur.

2) Placer sur la figure précédente :
• I, le point du segment [AD] tel que AI = 9.6 cm ;
• J, le point d’intersection de la droite (BD) et de la parallèle à (CD passant par I.

3) Calculer la distance DJ.

4) Calculer la distance JI.

Exercice 3

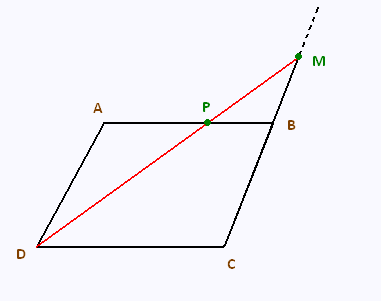
ABCD est un parallélogramme tel que AB = 6 cm et AD = 5 cm.

Les dimensions ne sont pas respectées sur la ?gure.

M est un point de [CB) tel que BM = 3 cm.
P est le point d’intersection des segments [AB] et [DM].

a) Calculer PB.
b) Calculer AP.

Exercice 4

1) Construire un triangle ABC tel que
AB = 8 cm ; AC = 12 cm et BC = 10 cm.

2) Soit M le point du segment [AB] tel que AM = 3.2 cm.
La parallèle à la droite (BC) passant par M coupe la droite (AC) en N.

Calcule la longueur AN.

Exercice 5

1) Construire un triangle ABC tel que AC = 7cm et AB = 6cm.
2) Placer le point P sur le segment [AB] tel que AP = 2cm. Tracer la parallèle à la droite (BC) passant par P : elle coupe le segment [AC] en un point R.
3) Mesurer AR.
4) Calculer la valeur exacte de AR.

Exercice 6

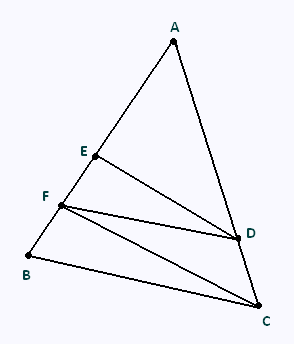
On donne :

• AE = 6 cm ;
• EF = 3 cm ;
• (FD)//(BC) ;
• (ED)//(FC).

1) Mettre des couleurs sur la figure ci-contre.

2) Coder cette figure.

3) Montrer que AD/AC = 2/3

4) Montrer que AF/AB = 2/3

5) Calculer FB.

Exercice 7

ABCD est un parallélogramme tel que :

AB = 8 cm ; AD = 12 cm et BD = 10 cm.

1) a) Faire une figure à main levée sur laquelle on écrira les longueurs.

b) Faire la figure en vraie grandeur.

2) Placer sur la figure précédente :

• P, le point du segment [AD] tel que AP = 9.6 cm ;
• Q, le point d’intersection de la droite (BD) et de la parallèle à (CD) passant par P.

3) Calculer la distance QD.

4) Calculer la distance PQ.

Exercice 8

Tracer un triangle ABC tel que :
AB = 6 cm, BC = 4 cm et AC = 5 cm.

1) Sur la demi-droite [AB), placer le point M tel que BM = 7 cm.
2) Tracer la parallèle à la droite (BC) passant par le point M ; cette droite coupe la droite (AC) en N.
3) Calculer la longueur MN.
4) Calculer la longueur CN.

Exercice 9

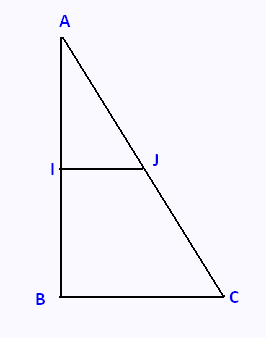
La figure ci-contre n’est pas en vraie grandeur. On demande pas de la reproduire.

Soit AIJ un triangle rectangle en I tel que IJ = 3.6 cm et IA = 4.8 cm.

On place le point B de la demi-droite [AI) tel que AB = 8 cm. La parallèle à la droite (IJ) passant par B coupe (AJ) en C.

1) Démontrer que AJ = 6 cm.

2) Calculer la valeur de AC, en justifiant la réponse.

Exercice 10

On considère UN triangle ABC rectangle en A tel que AB = 5, BC = 9, l’unité étant le cm.

1) Construire le triangle ABC en vraie grandeur.
2) Calculer la valeur de AC arrondie au mm.
3) Calcule la mesure de l’angle ABC à un degré près par défaut.
4) Le cercle de centre B et de rayon AB coupe le segment [BC] en M.

La parallèle à la droite (AC) qui passe par M coupe le segment [AB] en N.

a) Compléter la figure.
b) Calculer la valeur exacte de BN.
c) Calculer la valeur de BN arrondie au centième.

Exercice 11

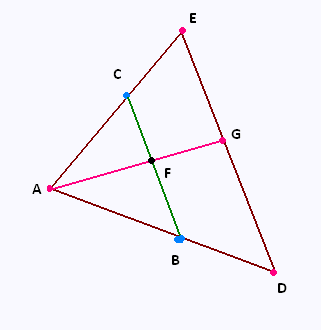Les dimensions ne sont pas respectées sur ce dessin.

Pour chaque question, on dessinera à main levée le triangle de travail.

Les droites (BC) et (DE) sont parallèles.

On donne :

AB = 5 cm, BC = 4 cm, BG = 3 cm,
DE = 7 cm et AF = 7.5 cm.

1) Montrer, par un calcul, que DG = 5.4 cm.
2) Montrer, par un calcul, que EC = 6cm.
3) Calculer CF.

Exercice 12

1) a) Tracer un triangle ABC tel que :
AB = 8 cm, AC = 15 cm et BC = 12 cm.

b) Placer le point I du côté [AB] tel que AI = 3.2 cm.
c) La parallèle à la droite (BC) passant par I coupe la droite (AC) en J.

La parallèle à la droite (AB) passant par J coupe la droite (BC) en K.

2) a) Calculer IJ.
b) En déduire que le quadrilatère BIJK est un losange.
c) Que peut-on en déduire pour les segments [IK] et [BJ] ?