Mathématiques: Géométrie
TRIGONOMETRIE
Exercice 1
ABC est un triangle tel que AB = 5 cm, BC = 13 cm et AC = 12 cm.
1) Faire une figure.
2) Montrer que CAB est un triangle rectangle.
3) Calculer l'angle ACB. On arrondira la valeur au degré près.
Exercice 2
ABCD est un rectangle de centre O tel que
AC = 12 cm et MES (∠ BOA) = 78o.
1) Faire une figure à main levée.
2) Calculer l’ensemble des angles de la figure
en utilisant les propriétés des angles d’un triangle.
3) Calculer AB.
4) Calculer BC.
5) A partir d’un cercle de diamètre [AC],
construire la figure et vérifier les réponses précédentes.
Exercice 3
On donne: cos θ = 0.45.
a) Calculer en degrés la mesure tronquée
à l'unité, de l'angle θ
b) Calculer la mesure de son complémentaire
φ
c) Calculer cos φ
d) Le côté adjacent à cet angle φ mesure 10 cm.
e) Construire à main levée un triangle rectangle,
puis placer les angles θ et φ.
f) Calculer la mesure de l'autre côté adjacent qui est
l'hypothénuse d'un triangle rectangle.
Exercice 4
Un triangle ABC est rectangle en A.
On donne :
AB = 5.8 cm et ∠ ABC = 62o.
1) Faire un schéma à main levée.
2) Calculer AB au millimètre près.
3) Calculer AC au millimètre près.
Exercice 5
Soit BAC un triangle tel que BA = 52 mm, AC = 39 mm et BC = 65 mm.
1) Montrer que le triangle BAC est rectangle.
2) Calculer l’angle ACB au degré près.
3) Construire le triangle BAC en vraie grandeur.
4) Mesurer l’angle ACB
Exercice 6
Soit (C) un cercle de diamètre [AB] mesurant 10 cm.
C est un point de (C) tel que BC = 6 cm.
D est un point de [AB] tel que AD = 3 cm.
Le cercle (C) de diamètre [AD] recoupe le segment [AC] en E.
1) Faire une figure en vraie grandeur.
2) Montrer que le triangle ABC est rectangle.
3) Calculer AC.
4) Montrer que les droites (DE) et (BC) sont parallèles.
5) Calculer DE.
6) Calculer une mesure de l’angle CBA.
Exercice 7
On donne cos x = 0.23.
a) Calculer en degrés la mesure, au centième près, de x.
b) Est-il possible de calculer cos-1 (x)? Justifier
Exercice 8
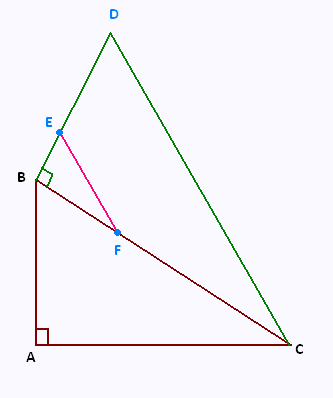
On donne les mesures suivantes:
mes (∠ CBD) = 90o ;
mes (∠ CAB) = 90o ;
mes (∠ CBA) = 55o ;
BD = 5 cm ; BC = 7 cm.
1) Calculer AC, puis en donner la valeur arrondie au
mm près.
2) Calculer la mesure de l’angle CDB en donnant sa valeur
arrondie à un degré près.
3) Les droites (EF) et (CD) sont parallèles et
BF = 2.5 cm.
Calculer BE. On donnera la valeur exacte
puis la valeur arrondie au mm près.
|