| Propriété |
Fonction (forme canonique) |
Exemple |
| |
 |
f(x) = ... |
| Coordonnées du sommet |
(h, k) |
... |
| Domaine (Dom f) |
• Si b > 0, dom f = [h, +∞[
• Si b < 0, dom f = ]- ∞, h[ |
dom f = ... |
| Image (Ima f) |
ima f = ...
|
| Variations |
• Si a > 0 et b > 0, f(x) est croissante dans [h, + ∞ [
• Si a < 0 et b > 0, f(x) est décroissante dans [h, + ∞ [
• Si a > 0 et b < 0, f(x) est décroissante dans ]- ∞, h]
• Si a < 0 et b < 0, f(x) est croissante dans ]- ∞, h]
|
• croissante dans ...
• décroissante dans ...
|
| Zéros de la fonction |
C'est la valeur z de x, tels que
f(x) = 0. Si elle existe. |
Le zéro est : z = ... |
| Ordonnée à l'origine |
Valeur de f(x = 0) |
f(0) = ... |
| Signe de la fonction f |
• f(x) est positive ou nulle dans
l'intervalle solution de l'équation f(x) ≥ 0.
• f(x) est négative dans
l'intervalle solution de l'équation f(x) < 0.
|
contrainte : ...
solution: ....
f(x) est positive ou nulle dans ....,
f(x) est négative dans ....
|
| Extremums |
• Si a > 0, la valeur minimale est k.
• Si a < 0, la valeur maximale est k.
|
La fonction a un max-minimum de .....
|
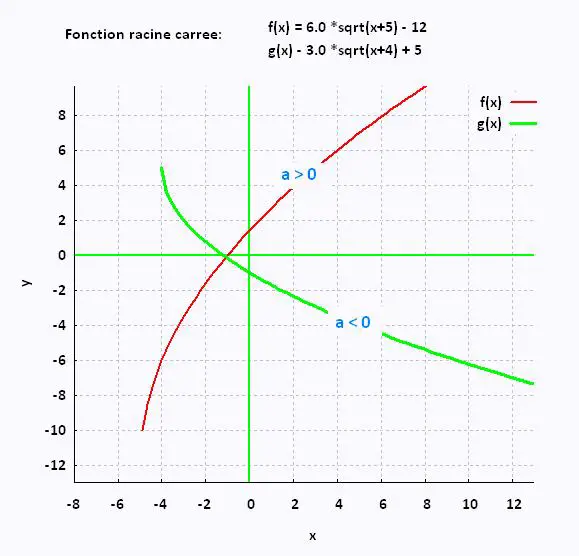
| Graphique de la fonction |
|

|


