Mathématiques
2
Propriétés des
nombres entiers
Calculateurs
Exercices de
perfectionnement
© The scientific sentence. 2010
| |
|
Mathématiques 2:
Les nombres entiers
Suite de Fibonacci
1. Leonardo Fibonacci

Leonardo Fibonacci (1175 - 1250) est un mathématicien italien.
Il est né à Pise en Italie. Son éducation s'est faite en grande partie
à Bjaya en Algérie, où son père était le représentant des marchands de
la république de Pise.
C'est dans cette ville Kabyle portuaire, qui est à l'époque un centre
commercial et intellectuel, que Fibonacci commence son éducation
en mathématiques. Il etudie notamment les travaux algébriques
d'Al-Khawarizmi.
Fibonacci pris conscience que les chiffres arabes et le système
décimal permettaient de manipuler les nombres plus aisément et
plus rapidement que le système des chiffres romains.
Ayant aussi voyagé au moyen orient pour le compte de son père,
et rencontré divers mathématiciens, Fibonacci en rapporta à Pise
en 1198 les chiffres arabes et la notation algébrique.
2. L'ouvrage de Fibonacci: Le Liber abbaci
L'ouvrage de Fibonacci est
Le Liber abaci (ou Liber abbaci) écrit en 1202. Ce titre signifie
Livre du calcul ou Livre de l'abaque. Il est l'un des premiers ouvrages
d'Europe occidentale.
Dans cet ouvrage, Fibonacci présente les chiffres arabes et le système
d'écriture décimale.
La première section présente les chiffres arabes et le système
d'écriture décimale positionnelle, y compris la technique de la multiplication
par jalousies et des méthodes pour passer d'un système de numérotation à l'autre.
La deuxième section introduit des exemples pour le commerce tels que la
conversion de monnaies et de mesures, le calcul du profit et de l'intérêt.
La troisième partie traite des problèmes mathématiques tels
que le théorème des restes chinois, le concept de nombre parfait, et
des formules mathématiques telles que la suite arithmétique ou le
nombre pyramidal carré.
Un exemple de suite mathématique donné dans ce livre, celui de la croissance
d'une population de lapins, est à l'origine de la suite de Fibonacci
pour laquelle l'auteur est principalement connu actuellement.
La quatrième section traite des approximations, numériques et géométriques,
de certains nombres irrationnels tels que les racines carrées.
Le livre inclut également des preuves en géométrie euclidienne et
une étude du système d'équations linéaires à la suite des travaux de Diophante
d'Alexandrie.
3. Suite de Fibonacci
La suite de Fibonacci est une suite d'entiers dans laquelle
chaque terme est la somme des deux termes qui le précèdent.
ou
La suite de Fibonacci est une suite d'entiers dans laquelle
chaque terme est la somme de son pénultième et de son antépénultième.
Elle commence généralement par les termes 0 et 1 (parfois 1 et 1)
et ses premiers termes sont :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ... etc...
Elle doit son nom à Leonardo Fibonacci qui, dans le problème
récréatif posé dans l'ouvrage Liber abaci,
décrit la croissance d'une population de lapins :
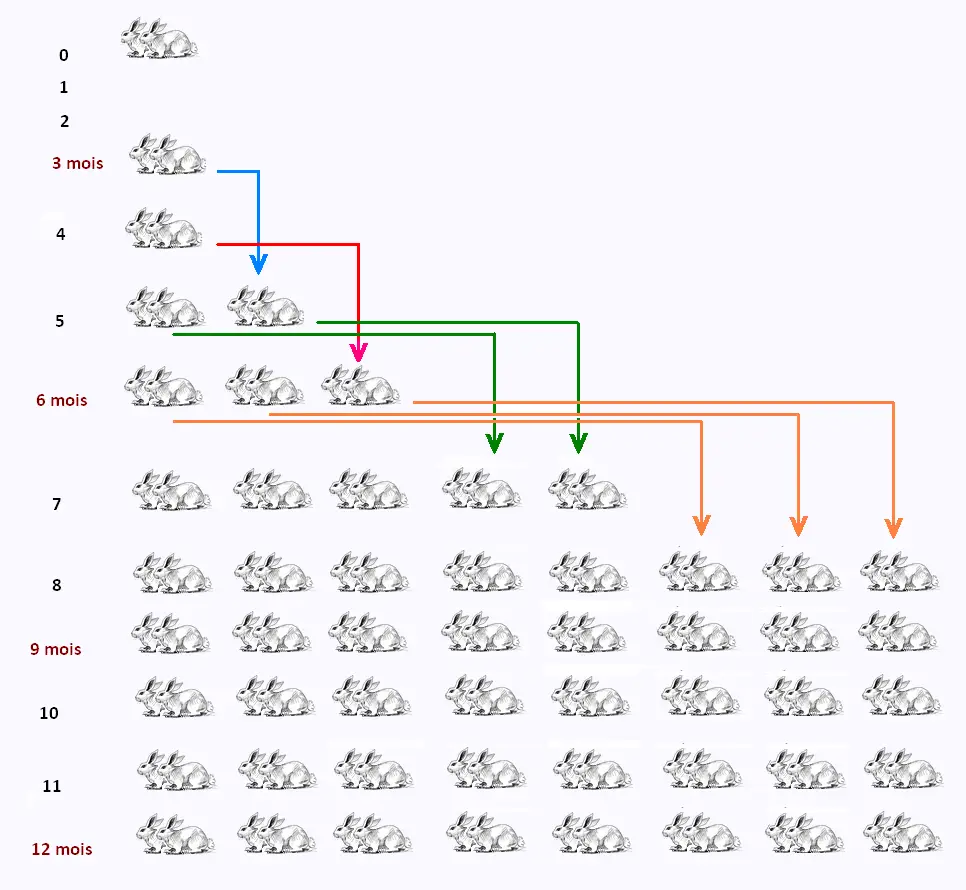
« Un homme met un couple de lapins dans un lieu isolé de tous les côtés
par un mur. Combien de couples obtient-on en un an si chaque couple engendre
tous les mois un nouveau couple à compter du troisième mois de son existence ? »
Dans cet énoncé. on suppose bien sûr qu'aucun lapin ne meurt pendant la durée du test,
et que chaque couple de lapins engendre chaque mois exactement un nouveau couple (un mâle
et une femelle) de lapins.
Dans la suite de Fibonacci les quotients de deux termes consécutifs
sont constant et valent approximativement 1.6 qui est le nombre d'or.
La suite d'entiers de Fibonacci est souvent utilisée en informatique
pour comprendre la récursivité.
Si on calcule le total de la population N de couples de lapins,
On peut en déduire qu'au mois x , la population N(x) est égale à la population
du mois prédcédent N(x - 1) plus la population deux mois auparavant N(x - 2).
Les seules exceptions sont les deux premières lignes du tableau, car
on doit attendre trois mois pour avoir le premier couple.
L'expression d'un terme de la suite de Fibonacci s'ecrit:
N(x) = N(x - 1) + N(x - 2)
où
N(x) est le terme de la suite de rang x.
|
|

