Mathématiques
2
Propriétés des
nombres entiers
Calculateurs
Exercices de
perfectionnement
© The scientific sentence. 2010
| |
|
Mathématiques 45: Arithmétique
La preuve par 9
1. Définition
La preuve par neuf est une technique qui permet de
vérifier un calcul de multiplication.
Cette technique peut juste montrer qu'un résultat est faux, mais
elle ne permet pas de conclure que le résultat est correct.
2. Le principe
La preuve par 9 s'appuie sur le modulo 9.
x = y mod(9) si 9 est le reste de la division de x par y.
Par exemple 16 = 7 mod(9).
Les 9 sont remplacés par des 0.
• On fait la multiplication des deux entiers a et b.
• On additionne les chiffres du nombre résultat trouvé,
on le note c,
• On additionne les chiffres du nombre a, on le note a1,
• On additionne les chiffres du nombre b, on le note b1,
• On fait la multiplication des deux entiers a1 et b1,
• On additionne les chiffres du nombre résultat trouvé,
on le note d,
Si c ≠ d, il ya une erreur, sinon il n'y a pas
d'erreur.
3. Exemple
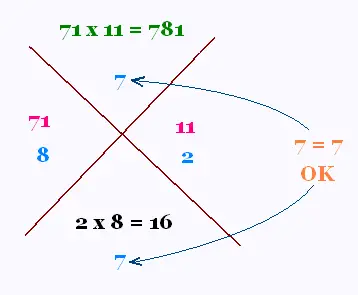
• On fait la multiplication des deux entiers 71 et 11,
• On additionne les chiffres du nombre résultat 781 trouvé,
7 + 8 + 1 = 16 = 7 on le note c = 7,
• On additionne les chiffres du nombre a = 71, on le note a1 = 8,
• On additionne les chiffres du nombre b = 11, on le note b1 = 2,
• On fait la multiplication des deux entiers a1 et b1 8 x 2 = 16,
• On additionne les chiffres du nombre résultat trouvé 1 + 6 = 7,
on le note d = 7,
c = d = 7. Il n'y a donc pas d'erreur dans le calcul de la
multiplication de 71 x 11 = 781.
|
|