Mathématiques 2: Arithmétique:
Résolution de problemes

1.Carreaux dans un rectangle

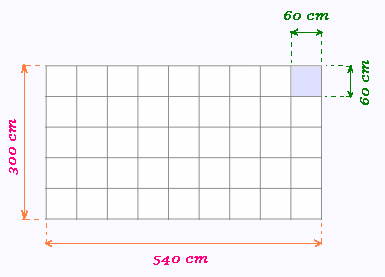
Soit un rectangle de 5.40 m de longeur et 3.0 m de largeur. On veut le recouvrir avec un nombre entier de carreaux.

Chaque carreau est un carré qui doit mesurer un nombre entier de cm.

Questions:

1) On veut que les carreaux soient de la plus grande taille possible:

a) Combien doit mesurer le côté de chaque carré?
b) Quel est le nombre de carreaux correspondant?


2) On veut que les carreaux soient de la plus petite taille possible:

a) Combien doit mesurer le côté de chaque carré?
b) Quel est le nombre de carreaux correspondant?

Réponses:

Les carreaux son évalués en cm, on convertit donc les dimensions du rectangle en cm :

Longeur = 5.40 m = 540 cm.
Largeur - 3.00 m = 300 cm

Soit c le côté du carreau.

Soit x le nombre de carreaux placés le long da la largeur de 300 cm. On a donc : x c = 300

Soit y le nombre de carreaux placés le long da la longeur de 540 cm. On a donc: y c = 540

c, x et y sont des entiers.

1)

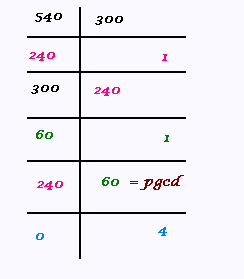
a) Le nombre entier c est un diviseur commun de 300 et de 540. Comme il doit être le plus garand possible, il est donc le PGCD de 300 et de 540:

Le pgcd de 540 et 300 est égal à 60.

Ainsi c = 60

Le carreau mesure 60 cm x 60 cm.

b) On en déduit donc

x = 300/60 = 5 carreaux le long de la largeur de 300 cm, et

y = 540/60 = 9 carreaux le long de la longeur de de 540 cm.


2) a) Le nombre entier c est un diviseur commun de 300 et de 540. Comme il doit être le plus petit possible, il est donc égal à 1:

Ainsi c = 1.

Le carreau mesure 1 cm x 1 cm.

b) On en déduit donc

x = 300/1 = 300 carreaux le long de la largeur de 300 cm, et

y = 540/1 = 540 carreaux le long de la longeur de de 540 cm, et

2. Assiette de fruits: clémentines et abricots

On dispose de 115 clémentines et de 69 abricots.

Afin de servir un dessert pour un groupe de personnes, on veut constituer des assiettes avec un maximum de ses fruits.

Chaque assiette doit contenir le même nombre de clémentines et le même nombre d'abricots.

Questions:

a) Combien d'assiettes au maximum peut-on constituer?
b) Combien de clémentines et d'abricots doit contenir une assiette ?

Réponses:

a) Le plus grang diviseur commun des 115 clémentines et des 69 abricots, c'est à dire leur pgcd est égal au nombre d'assiettes à constituer. Ce pgcd vaut 23 .

115 = 23 x 5
69 = 23 x 3

On peut donc constituer au maximum 23 assiettes.

b) Chaque assiette contient 5 clémentines et 3 abricots.

3. Des choses dans des sacs

Nous avons deux choses x et y à diviser et à répartir dans un maximum de sacs tous de contenu identique.

Le nombre de ses sacs est égal au pgcd(x,y).

Chaque sac doit cotenir:
• x/pgcd(x,y) de choses x et
• y/pgcd(x,y) de choses y.