Mathématiques
2
Propriétés des
nombres entiers
Calculateurs
Exercices de
perfectionnement
© The scientific sentence. 2010
| |
|
Mathématiques 45: Arithmétique
Recherche de deux nombres entiers connaissant
leur pgcd et leur ppcm.
1. Formule à utiliser
Comment trouver deux nombres entiers naturels connaissant
leur pgcd et leur ppcm?
Soient deux nonbres entiers naturels a et b.
Puisque le pgcd est un diviseur de a et b, on peut ecrire:
a = (pgcd) x m (1)
b = (pgcd) x n (2)
m et n sont premiers entre eux. (3)
On sait, d'autre part que:
pgcd(a, b) x ppcm(a, b) = a x b (4)
Multiplions (1) avec (2), on obtient:
(pgcd)2 x m x n = a x b
Avec l'équation (4), on obtient:
pgcd(a, b) x ppcm(a, b) = (pgcd)2 x m x n
ou
ppcm(a, b) = (pgcd) x m x n
Ainsi
le rapport du ppcm au pgcd de deux nombres entiers est égal
au produit des nombres premiers quotients de ces nombres par
leur pgcd.
Maintenant divisons a par b en utilisant les relations (1) et (2), on
obtient:
a/b = m /n
ou
a x n = b x m
Le problème revient donc à trouver deux nombres a et b tels que:
a x n = b x m
m = a/pgcd et n = b/pgcd
avec m et n premiers entre eux .
2. Exemple:
On cherche deux nombres entiers a et b connaissant
leur pgcd = 4 et leur ppcm = 280.
Nous avons:
ppcm/pgcd = 280/4 = 70 = m x n
On cherche donc deux nombres a et b tels que:
a = 4 x m et
b = 4 x n
en utilsant m x n = 70 ,
avec m et n premiers entre eux.
1) On prend m = 1 donc n = 70 : n'est pas la solution
parce que 1 et 70 ne sont pas premiers entre eux.
2) m = 2, donc n = 35: est une solution
parce que 2 et 35 sont premiers entre eux.
Donc a = 4 x 2 = 8 et b = 4 x 35 = 140
a = 8 et b = 140
3) m = 3, donc n = 70/3 : n'est pas la solution
parce que 70/3 n'est pas entier.
4) m = 4, donc n = 70/4: n'est pas la solution
parce que 70/4 n'est pas entier.
5) m = 5, donc n = 14: est une solution
parce que 5 et 14 sont premiers entre eux.
Donc a = 4 x 5 = 20 et b = 4 x 14 = 56
a = 20 et b = 56
6) m = 6, donc n = 70/6: n'est pas la solution
parce que 70/6 n'est pas entier.
7) m = 7, donc n = 10: est une solution
parce que 7 et 10 sont premiers entre eux.
Donc a = 4 x 7 = 28 et b = 4 x 10 = 40
a = 28 et b = 40
.....
10) m = 10, donc n = 7: est une solution
parce que 10 et 7 sont premiers entre eux.
Donc a = 4 x 10 = 40 et b = 4 x 7 = 28,
solution déjà trouvé au 7).
On s'arrête en fait au nombre m = 9. 9 est la racine carée
immédiatement suppérieure ou égale à √(m x n) =
√70 = 8.37 donc m = 9. Dans ce cas , on a tous
les cas possibles.
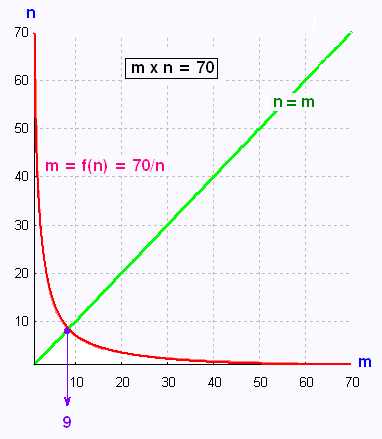
La droite d'équation n = m est l'axe de symétrie de la courbe
d'équation n = 70/m.
3. Execice 1:
Trouver deux nombres entiers a et b connaissant
leur pgcd = 18, et leur ppcm = 3780.
Compléter la séquence de calcul suivant:
ppcm/pgcd = 3780/18 = 210 = m x n
On cherche donc deux nombres a et b tels que:
a = 18 x m et
b = 18 x n
en utilsant m x n = 210 ,
avec m et n premiers entre eux.
1) On prend m = 1 donc n = 210 : n'est pas la solution
parce que 1 et 210 ne sont pas premiers entre eux.
2) m = 2, donc n = 105: est une solution
parce que 2 et 105 sont premiers entre eux
Donc a = 18 x 2 = 36 et b = 18 x 105 = 1890
a = 36 et b = 18
3) m = 3, donc n = 70 : est une solution
parce que 3 et 70 sont premiers entre eux
Donc a = 18 x 3 = 54 et b = 18 x 70 = 1260
a = 54 et b = 1260
...
 On s'arrête au nombre m
immédiatement suppérieur ou égal à √210 = 14.49,
c'est à dire m = 15. On s'arrête au nombre m
immédiatement suppérieur ou égal à √210 = 14.49,
c'est à dire m = 15.
3. Execice 2:
Soient trois entiers naturels a, b, et z.
Démontrer que :
si pgcd(a, b) = 1, alors
pgcd(z, a x b) = pgcd(z, a) x pgcd(z, b)
Réponse:
On considère trois entiers naturels
z, a et b
avec a et b premiers entre eux.
Soit gaz le pgcd(a, z) et
gbz le pgcd(b, z).
on peut donc ecrire:
a = gaz x A et
b = gbz x B
A et B sont premiers entre eux puisque
a et b le sont.
Le produit ab donne:
ab = gaz x gbz x A x B
A et B sont premiers entre eux donc
gax x gbx est égal au pgcd (x, ab).
Or gaz x gbz =
pgcd(a, z) x pgcd(b, z)
Donc
pgcd(z, ab) = gaz gbz = pgcd(a, z) x pgcd(b, z)
Ainsi
 Vérifier vos résulats par ce logiciel Vérifier vos résulats par ce logiciel
|
|